티스토리 뷰
Experiment220428_PCA, K-Means, Linear Interpolation
dancefirst 2022. 4. 28. 18:31### Context.
* 기본적으로 3D 키프레임 제작은 주요 동작을 생성한 뒤, 선형보간으로 사이 프레임을 메꾸는 방식
* 선형보간을 통해 연속적인 키프레임 포즈 데이터에 대한 보간이 가능하다
### Experiment.
* ROMP - OneEuro 결과물에 대해 PCA Clustering 수행
* 핵심이 되는 / 다른 군집과 차별되는 n개의 pose keyframe 및 해당 키프레임 인덱스 추출
* 인덱스 사이에 빠져 있는 키프레임을 high order interpolation으로 보간
해당 실험에 사용할 모션 데이터를 추출한 원본 비디오, 및 모션 데이터 리타겟팅 샘플은 아래와 같다. 아래 영상은 33fps 기준 총 242개의 프레임으로 구성되었으며, 모션 데이터 또한 동일하다.

import os
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
from sklearn.preprocessing import StandardScaler
from sklearn.cluster import KMeans
from sklearn.decomposition import PCA
# import motion data
path_dir = './portfolio/giphy_npz/sample2/'
path_filename = 'bpYI04FUNB6fu_400_225_33_results_opt.npz'
path = os.path.join(path_dir, path_filename)
sample = np.load(path, allow_pickle=True)['results'][()]
sample_keys = list(sample.keys())
sample_poses = np.array([sample[key][0]['poses'] for key in sample_keys])
# standardize
scaler = StandardScaler()
# segmentation_std = scaler.fit_transform(sample_poses_reshape)
segmentation_std = scaler.fit_transform(sample_poses)
# PCA
pca = PCA()
# pca.fit(segmentation_std)
pca.fit(segmentation_std)
주성분 갯수를 결정하기 위해 시각화한다.
plt.figure(figsize=(10,8))
plt.plot(range(1,73), pca.explained_variance_ratio_.cumsum(),
marker='o', linestyle='--')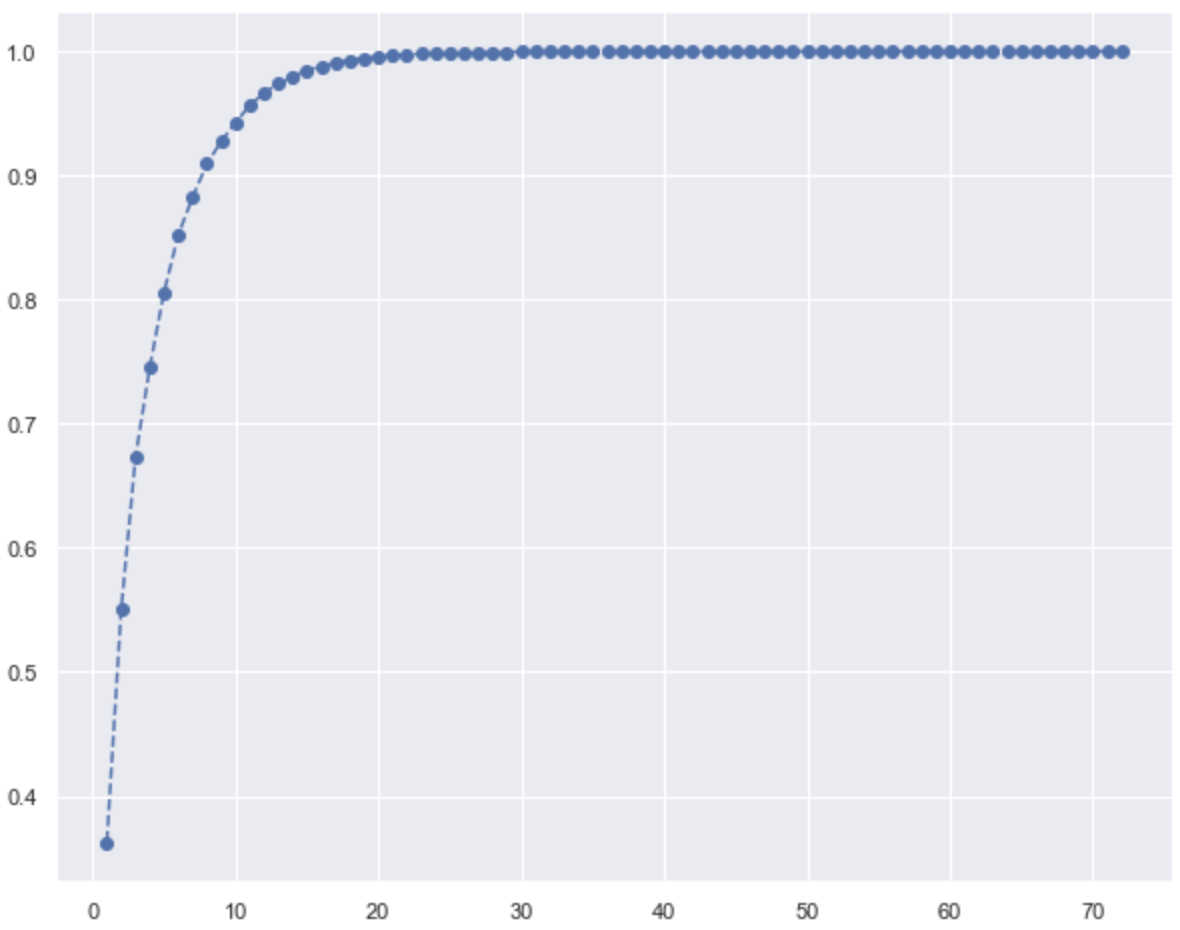
A rule of thumb is to preserve around 80 % of the variance. So, in this instance, we decide to keep 5 components.
pca = PCA(n_components=5)
pca.fit(segmentation_std)
scores_pca = pca.transform(segmentation_std)
# K-means clustering with PCA, up to 20 clusters
wcss = []
for i in range(1, 21):
kmeans_pca = KMeans(n_clusters=i, init='k-means++', random_state=33)
kmeans_pca.fit(scores_pca)
wcss.append(kmeans_pca.inertia_)
K-Means 클러스터 갯수를 결정하기 위해 시각화한다.
# plotting the WCSS against the number of components on a graph.
plt.figure(figsize=(10,8))
plt.plot(range(1,21), wcss, marker='o', linestyle='--')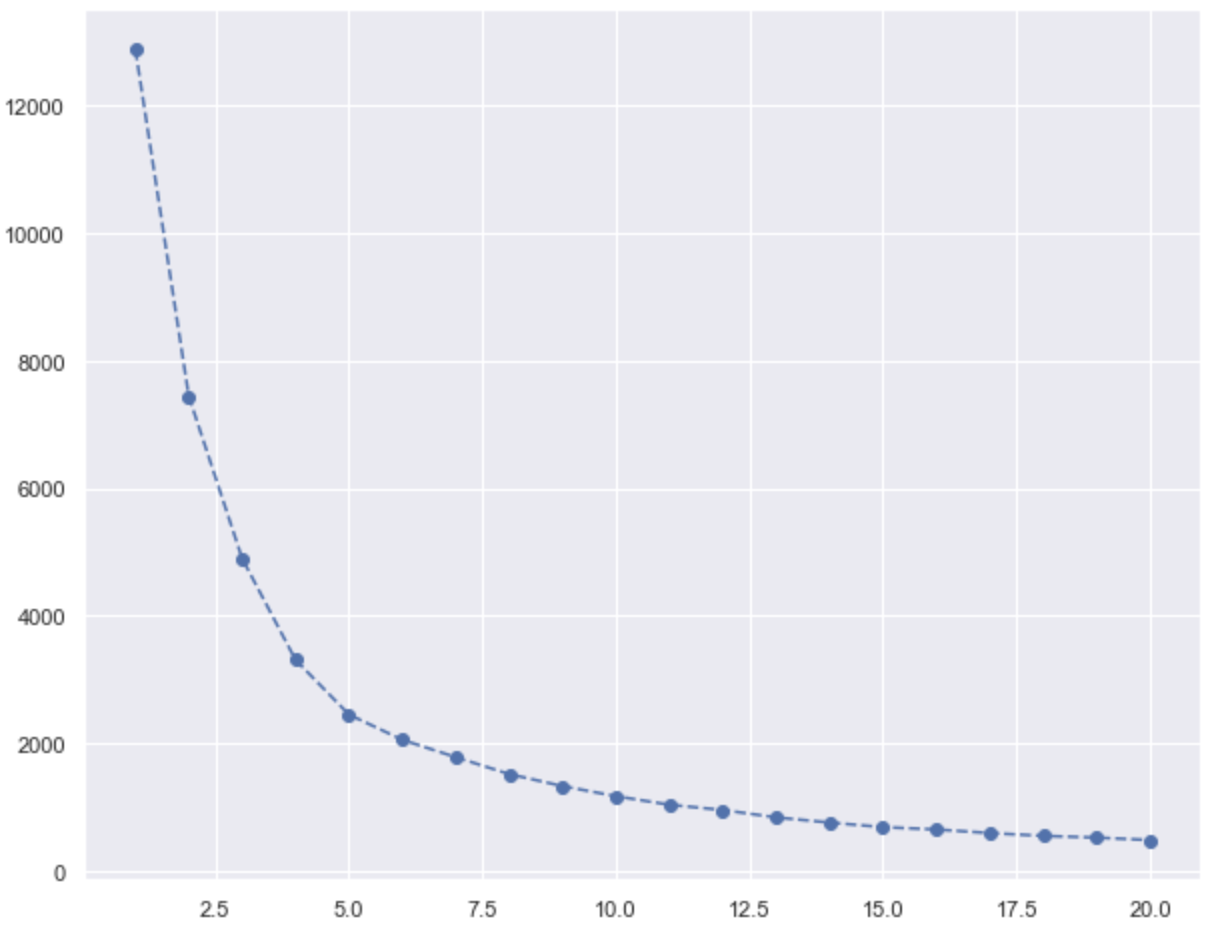
# n_clusters=6
kmeans_pca = KMeans(n_clusters=6, init='k-means++', random_state=33)
PCA 주성분 5개를 기준으로 n_clusters=6 파라미터로 K-Means를 수행, 모션 데이터를 구성하는 pose 데이터를 군집화 결과에 따라 나누어 준다.
arr_seg_pca_kmeans = np.concatenate((sample_poses, scores_pca), axis=1)
arr_seg_pca_kmeans = np.concatenate((arr_seg_pca_kmeans, kmeans_pca.labels_.reshape(kmeans_pca.labels_.shape[0], 1)), axis=1)
# arr_seg_pca_kmeans.shape
242개의 프레임에 대해 수행된 클러스터 라벨 출력값은 다음과 같다.
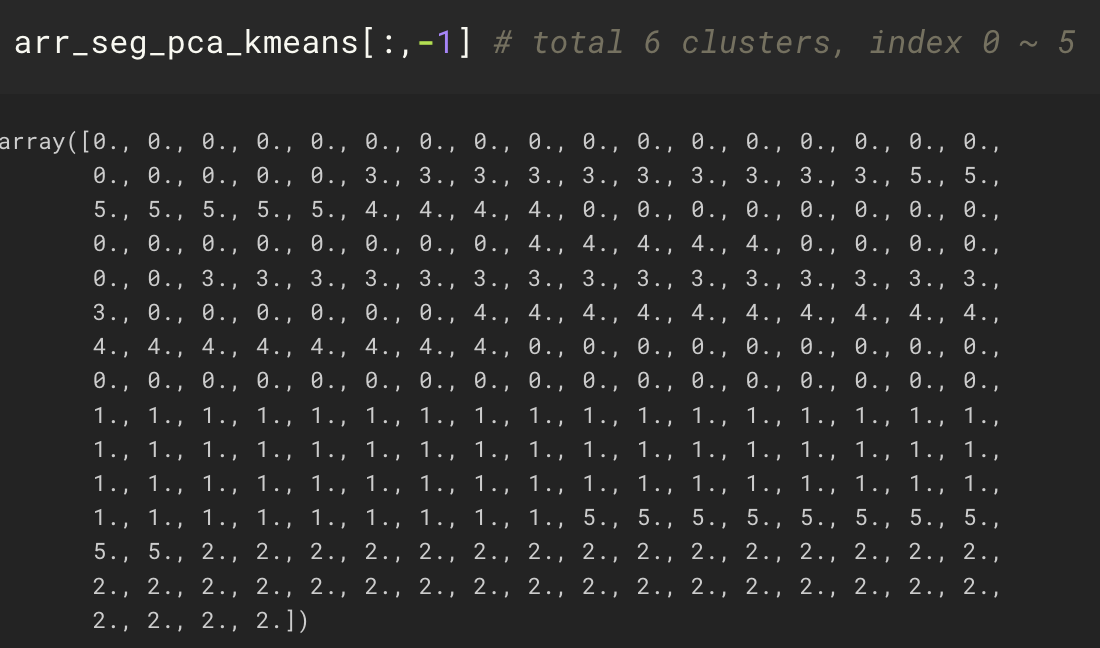
동일한 값으로 이루어진 개별 군집들을 분리하기 위한 함수를 작성, 적용한다.
# cluster 단위로 키프레임 구간 나눠주기.
def extract_cluster_indices(pca_labels):
prev_pca_label = pca_labels[0]
current_cluster_indices, total_cluster_indices = [], []
for i, pca_label in enumerate(pca_labels):
is_last_element = i + 1 == len(pca_labels)
is_same_with_prev_label = pca_label == prev_pca_label
if not is_last_element:
if is_same_with_prev_label:
current_cluster_indices.append(i)
else:
prev_pca_label = pca_label
total_cluster_indices.append(current_cluster_indices)
current_cluster_indices = []
current_cluster_indices.append(i)
else:
if is_same_with_prev_label:
current_cluster_indices.append(i)
total_cluster_indices.append(current_cluster_indices)
else:
total_cluster_indices.append(current_cluster_indices)
total_cluster_indices.append([i])
return total_cluster_indices
cluster_ids = extract_cluster_indices(arr_seg_pca_kmeans[:,-1])
pelvis joint의 z 좌표값을 예시로 하여 원본 데이터와 linear interpolation 결과를 시각화 해 본다. 이 때, linear interpolation은 첫번째와 마지막 프레임의 포즈 데이터에 대해 수행되며, 첫 22개 프레임으로 구성된 첫번째 클러스터로 한정된다.
first_cluster_poses = sample_poses[cluster_ids[0]] # 1번 클러스터에 해당하는 원본 포즈데이터
first_cluster_poses_recon = np.linspace(first_cluster_poses[0], first_cluster_poses[-1], first_cluster_poses.shape[0]) # linear interpolation
# visualize of first element (pelvis z coordinate)
plt.plot(first_cluster_poses[:, 0])
plt.plot(first_cluster_poses_recon[:, 0])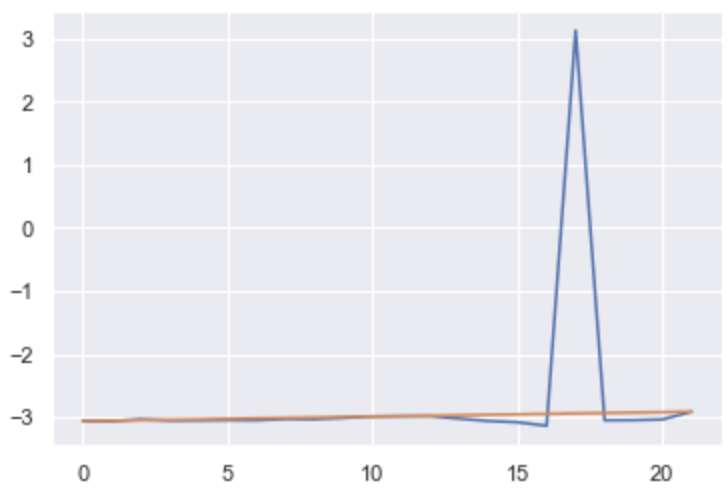
예상대로, 원본의 데이터에는 값이 급격하게 변화하는 아웃라이어가 존재하지만 linear interpolation의 경우 첫번째 값과 마지막 값을 기준으로 단순 직선형으로 나타난다.
첫번째 클러스터에 해당하는 모든 관절들의 포즈 데이터를 원 자료형으로 재구성하여, 최종적으로 결과물을 시각화 해 본다.
original_pose_npz = np.load(path, allow_pickle=True)['results'][()]
recon_pose_npz = np.load(path, allow_pickle=True)['results'][()]
# inner_keynames = list(original_pose_npz[sample_keys[0]][0].keys())
# 원하는 키프레임 정보만 남긴다
for key_id, keyname in enumerate(sample_keys):
if key_id in cluster_ids[0]:
# cam_trans, betas, poses 정보만 남긴다
# for inner_keyname in inner_keynames:
# if inner_keyname not in ['cam_trans', 'betas', 'poses']:
# del original_pose_npz[keyname][0][inner_keyname]
# del recon_pose_npz[keyname][0][inner_keyname]
# poses 데이터 수정 (only for reconstruct)
recon_pose_npz[keyname][0]['poses'] = first_cluster_poses_recon[key_id]
# print((recon_pose_npz[keyname][0]['poses'] == first_cluster_poses_recon[key_id]).all())
else:
del original_pose_npz[keyname]
del recon_pose_npz[keyname]
# export as npz file
save_dir = './output/interpolation'
np.savez(os.path.join(save_dir, 'test_original.npz'), results=original_pose_npz)
np.savez(os.path.join(save_dir, 'test_recon.npz'), results=recon_pose_npz)
블렌더 상에 SMPL 표준 모델로 두 포즈 데이터를 import, 렌더링한 결과는 아래와 같다. 좌측이 원본의 첫번째 클러스터에 해당하는 포즈 데이터, 우측이 linear interpolation으로 재구성한 첫번째 클러스터의 포즈 데이터의 결과물이다.
첫번째 클러스터 구간은 겨우 22개 프레임만으로 구성되지만, 원본의 경우 상당히 복잡한 움직임을 포함하고 있다. 첫번째 클러스터의 첫 프레임과 마지막 프레임을 단순 선형보간한 우측 결과물은 원본에 비하여 훨씬 부드럽지만 극도로 단순화된 움직임만을 표현한다.
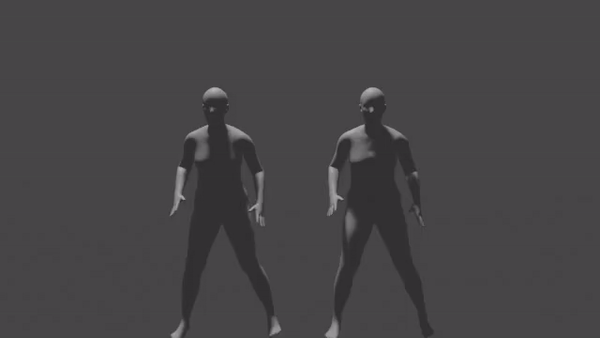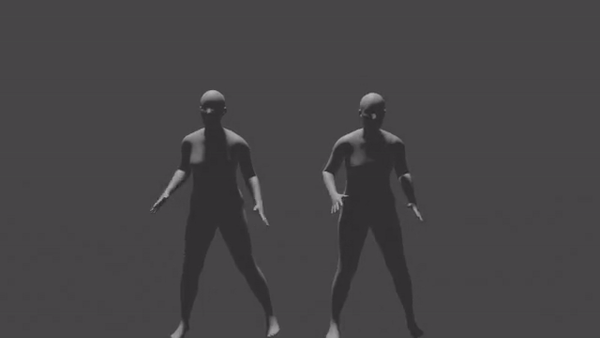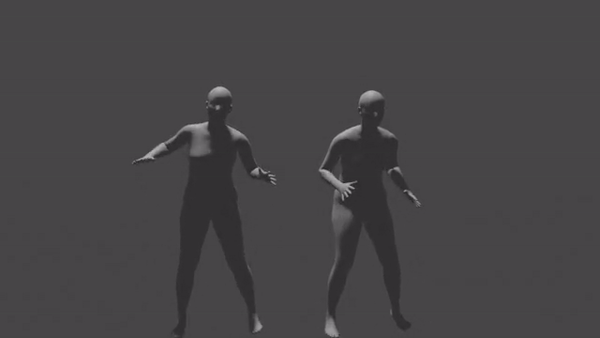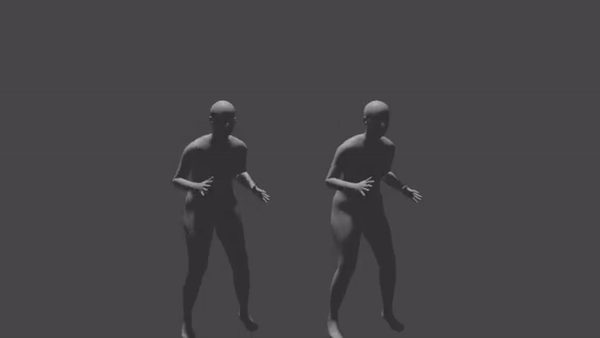
[결론]
가장 단순한 방법으로 접근한 이번 실험을 통해 알게된 것, 추가적으로 고려할 것 및 진행해야 할 사항은 다음과 같다.
* PCA + K-Means 파라미터 결정을 기존 rule of thumb에 따라 진행할 경우, 포즈 데이터의 복잡성을 충분하게 포착하지 못한다. 위 결과를 통해 알 수 있듯, 첫번째 클러스터는 육안으로 보았을 때 추가적으로 2-3개 이상의 서브 클러스터로 세분화될 수 있어 보인다.
* 서브 클러스터링이라는 접근 방법을 고려할 수 있다. 1차적으로 선별된 6개 클러스터의 포즈 데이터에 대해, 우리는 분산 등의 통계치를 활용하여 얼마나 복잡한 움직임이 해당 클러스터에서 발생하는가를 판단할 수 있다. 이러한 정보를 추가적으로 활용하여 클러스터의 갯수를 늘린다. 즉, 전체 포즈 데이터를 더 잘게 나눈 뒤 선형보간을 실시한다. -> variance-adaptive interpolation.
* variane-adaptive 관점의 서브 클러스터링 접근에 있어서 "움직임이 급격하게 변화하는 포인트"를 정확하게 포착하고 이를 서브 클러스터링으로 연계하는 것이 대단히 중요할 것.
* 한편, 1차 함수로서의 단순 선형 보간은 직관적으로 생각해 보아도 인체 모션 적용에 한계가 있다. 설령 서브 클러스터링이 잘 수행된다 하더라도, 1차 선형 보간을 적용한다면 비연속적인 그래프가 형성되어, 최종 시각화 결과 움직임이 뚝뚝 끊어지게 보일 것이다. 따라서, 보다 연속적인 방식의 결과물을 도출하는 보간을 고려할 필요가 있다.
'AI Motion Capture > Works' 카테고리의 다른 글
| Experiment220430_PCA, K-Means, Linear Interpolation(2) (0) | 2022.04.30 |
|---|---|
| Pre-analysis for ROMP joint data (0) | 2022.04.12 |
- Total
- Today
- Yesterday
- 3d affine transform
- 고려대학교 한정현
- tensorflow.js
- 메타버스
- vertex shader
- 원유로필터
- 컴퓨터그래픽스
- 컴퓨터그래픽스 좌표계와 변환
- 컴퓨터그래픽스 강의
- PoseNet
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
