One Euro Filter 논문 번역

 

노이즈 처리 알고리즘 One Euro Filter 논문에 대한 명확한 이해를 위해 전문을 번역하여 포스팅합니다.

---

 

ABSTRACT

원유로 필터(1€ filter)는 높은 정확성과 반응성을 위해 신호 노이즈를 필터링하는 단순한 알고리즘이다. 원유로 필터는 adaptive cutoff frequency를 적용하는 1차(first order) 로우패스 필터를 사용한다. 신호의 변화 속도가 느릴 경우, 낮은 cutoff를 적용함으로써 jittering을 줄이고 신호를 안정화한다. 반대로 신호의 변화 속도가 빠를 경우, cutoff를 증가시켜서 지연(lag)을 감소시킨다. 이 알고리즘은 구현하기 쉽고, 컴퓨팅 리소스가 거의 들지 않으며, 이해하기 쉬운 2개의 파라미터만을 사용하여 튜닝이 용이하다. 다른 노이즈 필터와 비교해서 원유로 필터는 동 수준의 jittering 감소를 달성하면서도 지연 현상은 덜 발생한다.

 

ACM Classification Keywords

H.5.2 [Information interfaces and presentation]: User interfaces - Input devices and strategies.

 

General Terms

Algorithms, Performance, Human Factors

 

Author Keywords

Signal; noise; jitter; precision; lag; responsiveness; filtering

 

INTRODUCTION

신호 잡음은 원본 시계열 값이 외부 영향으로 예기치 않게 소폭 변화(perturbations)할 때 발생한다.  이러한 변화는 하드웨어 회로에 열기나 전자기장이 영향을 미치거나, 센서 해상도가 제한되거나 수치연산이 일관적으로 수행되지 않는 등의 이유로 발생한다. 신호 잡음은 인체 동작 추적(human motion tracking) 분야에서 흔히 문제이며, 특히 자체 개발한 센싱 하드웨어나 Kinect, Wiimote 등 저렴한 입력 디바이스를 사용할 때 많이 발생한다. 더욱이, 하이엔드 급의 고가 센싱 시스템이 출력하는 신호 또한 라지 스케일링 효과로 인해 잡음이 생길 수 있다. 대표적인 예시로는 벽면 디스플레이에 레이 캐스팅을 구현하는 Vicon 트래킹 시스템이 있다. 측정오차 및 손떨림 등의 변수가 추가적인 perturbation으로 작용, 기본적으로 발생하는 신호 잡음을 증폭시키게 된다.

 

신호 잡음은 주로 2가지 방법으로 신호 품질에 영향을 미친다. 첫째로 신호 잡음은 관측값과 실제값 간의 오프셋(간격, 격차)을 발생시킴으로써 정확성(accuracy)을 감소시킨다. 둘째, 반복적으로 관측되는 값들이 jitter 현상을 일으켜서 정확도(precision)를 떨어트린다. jitter란, 실제값은 하나일지라도 매우 다양한 수치로 표현되는 현상을 말한다. Jitter 현상은 사람들이 인식하고 행동하는 방식에 큰 영향을 미친다. 예를 들어, 잡음이 섞인 신호들은 판독하기가 더 어렵고, 불안정한 커서는 target acquisition을 방해한다. 이러한 이유들로 신호 잡음을 줄이거나 가능하다면 아예 없애기 위해 필터를 사용하게 된다. 하지만 필터링 기법은 내재적으로 흔히 랙(lag)이라고 불리는 시간 지연을 일으키고, 이로 인해 시스템 responsiveness를 감소시킨다. 시간 지연은 감각정보 인식-해석(artifical perception) 또는 의사결정 분야에서 큰 문제가 아니지만, 피드백을 주고받는 상호작용 시스템에서는 매우 중대한 문제가 된다. 사실 중요한 것은 precision과 responsiveness의 결합이다. 사람들은 노이즈로 인한 오프셋이 발생하더라도 어느정도 정확하게 대상을 포인팅할 수 있겠지만, 이는 lag과 jitter가 최소화될 때 가능하다. 이러한 jitter와 lag 문제를 최소화하는 필터를 구현하고 튜닝하는 문제는 해결하기 쉽지 않으며, 특히 신호처리 분야에 지식이 거의 없는 경우는 더욱 힘들다.

 

본 논문에서 우리는 원유로 필터(1€ filter)를 제시한다. 원유로 필터는 jitter-lag 밸런스를 조정 가능하면서 신호 잡음을 개선할 수 있는 도구다. 원유로 필터는 로우패스 필터를 사용하지만, cutoff frequency 값이 속도에 따라 변화한다. 속도가 느릴 때 cutoff는 낮아지고, lag을 희생하는 대신 jitter를 감소시킨다. 반대로 속도가 빠를 때 cutoff는 높아져서 jitter 대신 lag을 감소시킨다. 이러한 로직에 담긴 직관은 다음과 같다. 움직임이 느릴 때 인간의 시각은 latency보다 jitter에 민감하게 반응하지만, 움직임이 빨라질 때 인간의 시각은 jitter보다 latency에 민감하게 반응한다. 우리는 원유로 필터를 다른 필터 기법과 비교하고, 동일 수준의 jitter를 감소시키면서 lag 또한 더 적게 억제할 수 있음을 보일 것이다. 원유로 필터는 또한 효율적이며 이해, 구현, 나아가 튜닝하기 쉽다. 단 몇 줄로 알고리즘을 표현할 수 있고 단순한 사칙연산을 사용한다. 그리고 jitter와 lag에 직접적으로 관여하는 두 개의 파라미터만을 갖는다. 우리를 포함한 여러 다른 연구자들은 원유로 필터를 다양하게 응용하여 여러 프로젝트에 활용하고 있다. 사실, "dynamic recursive low-pass filter" 연구가 기본적인 원칙을 정립했지만, 파라미터가 4개라는 점과 샘플 레이트가 고정적이라는 한계를 갖고 있었다. '원유로(1€)'라는 이름은 '$1 recognizer'에 대한 오마쥬이며, 우리는 $1 recognizer가 제스쳐의 영역에서 큰 개선을 이루었듯 원유로 필터가 입력 신호를 단순화하고 개선해낼 수 있다고 생각한다.

 

본 논문에서는 jitter, lag 그리고 현존하는 다른 필터링 기법들을 먼저 살펴본다. 그 후 우리는 원유로 필터를 구현법과 함께 상세하게 살펴보고, 다양한 적용 상황에서의 튜닝을 논한 뒤 수치화된 비교에 근거해 결론을 내릴 것이다.

 

JITTER, LAG, AND FILTERING

여러 연구들은 jitter와 lag이 퍼포먼스에 부정적인 영향을 미친다는 것을 보였다. MacKenzie et al. 의 경우 마우스 이동시간이 75ms lag일 때 16%, 225 ms lag일 때 64% 증가한다는 것을 발견했다. 3D 핸드 트래킹의 경우, Ware & Balakrishnan은 고작 50ms의 lag이 전체 성능을 8% 이상 감소시킨다는 것을 발견했다. Pavlovych & Stuerzlinger는 마우스나 Wiimote 기준으로 58ms lag 미만에서 성능 저하가 없음을 확인했지만, jitter를 4픽셀에서 8픽셀로 증가시켰을 때 작은 타깃에 대해 에러율이 2배 상승함을 발견했다. 100 PPI 스크린을 가정했을 때 4픽셀 jitter는 mean-to-peak 1mm에 대응하는데, 이는 상용 Optitrack 시스템에서 관측된 0.4mm jitter에 근접한 수치다.

 

입력 디바이스의 precision 성능이 매우 좋을지라도, 이는 상호작용 환경에서 발생하는 스케일링 효과까지 반영하지는 않는다. 장치의 입력값은 종종 더 큰 값으로 스케일링되며, 따라서 사람이 디바이스를 더 적게 움직여도 더 넓은 디스플레이 거리를 커버하게 된다. 예를 들어, 기본 운영체제의 마우스 전송 함수들은 최대 12배까지 스케일 업 될 수 있으며, 벽면 크기의 디스플레이에 레이캐스팅할 때 스케일 팩터는 90배까지 상승한다. 장치의 precision과는 상관없이 스케일링 팩터는 아주 작은 센싱 오차조차도 크게 증폭시키게 되며 결과적으로 jitter가 증가한다.

 

이러한 결과들은 jitter-lag 간의 균형이 매우 중요함을 시사한다. jitter는 1mm mean-to-peak 밑으로 억제되어야 하지만, lag 또한 60ms를 넘어서는 안 된다. 후술하겠지만 노이즈 필터는 종류와 상관없이 lag을 발생시키게 되는데, 시스템 자체의 lag이 40-50ms라고 가정할 때 필터의 허용한계치는 10-20ms lag가 된다.

 

Moving Average

중심극한정리(Central Limit Theorem)과 기타 가정들에 의해, 신호 잡음에서 충분히 많은 연속적인 값들을 평균냄으로써 실제 신호값을 추정할 수 있다. 결과적으로, 직전 n개 데이터에 대한 moving average 연산은 일종의 필터로서 컴퓨터 과학자들이 흔히 사용하는 기법이다. 예를 들어, Myers et al.은 레이저 포인터 신호에 moving average를 적용, 손떨림으로 인한 jitter를 +-8픽셀에서 +-2~4 픽셀로 줄일 수 있었다(0.5s window, n = 10). 모든 n개의 신호값들은 동일 가중치를 부여받으므로, sampling period 최대 n배까지의 lag을 발생시키게 된다.

 

Low-pass filters and exponential smoothing

인체 모션 노이즈는 일반적으로 신호에 high frequencies를 만들어내는 반면, 팔다리의 움직임은 더 낮은 frequency를 갖는다. 로우패스 필터는 이러한 정상 low frequency 부분들은 그대로 보존하되 고정된 cutoff frequency를 초과하는 high frequency 신호들을 낮게 조정(attenuate)하도록 고안되었다. 로우패스 필터의 차수(order)는 각 frequency를 얼마나 강력하게 제어하는가에 직접적으로 영향을 미친다. 1차 로우패스 필터는 frequency가 2배가 될 때마다 신호값의 높낮이(amplitude)를 절반으로 낮춘다. 2차 이상의 변형 로우패스 필터는 신호 높낮이를 더 큰 비율로 감소시킨다. 1차 로우패스 필터의 discrete time realization(아날로그->디지털 변환)은 아래 방정식1을 따르며, notation은 다음과 같다.

 

• \(x_i\) raw data at time \(i\)
• \(\hat{x}_i\) filtered data t time \(i\)
• \(\alpha\) smoothing factor in [0, 1]

Equation [1]

$$ \hat{X}_i = \alpha X_i + (1 - \alpha) \hat{X}_{i-1} $$

 

위 방정식의 첫번째 항은 새로운 입력 데이터의 기여분이며, 두번째 항은 직전 입력 데이터의 관성 영향치를 더해준다. \(\alpha\)가 감소할수록 jitter는 감소하지만 lag이 증가하는데, 출력값이 입력값의 변화에 더 느리게 반응하게 되기 때문이다. 이전 데이터 값들이 반영되는 정도는 지수적으로 감소하기 때문에, 로우패스 필터는 \(n\) moving average 필터보다 lag이 더 적게 발생하게 된다.

 

비즈니스와 경제 영역의 예측에 사용되는 스무딩 기법은 로우패스 필터와 접근 방식에서 유사하다. single exponential smoothing 방정식은 앞서 살펴본 1차 로우패스 필터 방정식과 매우 비슷하다. 이름에서 알 수 있듯, double exponential smoothing은 신호의 추세를 처리하는 데 방정식 2개를 사용한다. 공식적으로 문서화되지는 않았지만, 마이크로소프트 Kinect의 스켈레톤 필터는 이러한 스무딩을 응용한 형태인 것으로 추정된다(http://cm-bloggers.blogspot.com/2011/07/kinect-sdk-smoothing-skeleton-data.html). LaViola는 double exponential smoothing을 예측 트래킹 목적으로 응용했는데, Equation 1, 2를 묶어서 미래의 \(\tau\) time steps를 예측하도록 했다.

 

Equation [2]

$$ \hat{X}_i^{[2]} = \alpha \hat{X}_i + (1-\alpha) \hat{X}^{[2]}_{i-1} $$

 

Equation [3]

$$ P_{t+\tau} = (2+\frac{\alpha\tau}{1-\alpha})\hat{X}_i-(1+\frac{\alpha\tau}{1-\alpha})\hat{X}^{[2]}_i $$

 

Kalman filters

상술한 기법과는 달리, 칼만 필터는 신호를 생성하는 시스템에 대한 가정에서 출발한다. 전형적으로 내비게이션과 트래킹에 활용되는 칼만 필터는 GPS + speedometer와 같이 상이한 센서로부터 획득한 데이터를 결합하는 상황, 또는 시스템이 방정식으로 모델링 가능(엑셀 페달 위치로부터 차량 가속량을 결정하는 등)한 상황에서 잘 작동한다. 칼만 필터는 process model과 measurement model에 기반한다. 표준 칼만 필터는 process model에 대하여 discrete-time linear stochastic 미분식을 사용하며, process / measurement 노이즈가 1)상호 독립적이며, 2)주파수 범위가 균일한 백색잡음이며, 3) 정규분포를 따른다고 가정한다. 움직이는 물체의 진짜 위치를 추정할 때 process model은 전형적으로 속도와 직전 위치 추정값에 대한 선형 함수를 사용한다. 이를 응용한 Extended / Unscented 칼만 필터는 비선형 프로세스와 관측을 모델링할 수 있다.

 

process 및 measurement 노이즈 공분산을 알 수 없는 경우에는 경험적으로 노이즈 공분산을 결정해 주어야 한다. 이러한 작업은 난이도가 높고, 부적절하게 튜닝된 필터는 "오버슈팅" 움직임을 만들어내는 등 신호를 인위적으로 증폭하기도 한다. 결과적으로 품질을 떨어트릴 수 있다. 게다가, 칼만 필터를 이해하기 위해서는 통계, 랜덤 신호, stochastic 기법 등 기본 선형대수 이상의 수리통계적 지식이 필요하다. 칼만 필터를 구현하기 위해서는 매트릭스 연산을 지원하는 언어나 라이브러리가 필요해진다. 또한, 예측 트래킹 알고리즘인 LaViola에서 적용된 double exponential smoothing 기법과 비교했을 때 jitter-lag 퍼포먼스는 유사하지만 연산속도는 약 135배 느리다.

 

THE 1€ FILTER

원유로 필터는 adaptive하게 작동하는 1차 로우패스 필터다. 원유로 필터는 각각의 새 샘플에 대해서, 신호 속도의 추정값 또는 그 미분값에 따라 로우패스 필터의 cutoff frequency를 조정하는 방식으로 작동한다. 신호 잡음은 종종 고정 frequency로 샘플링되기도 하지만, 항상 같은 페이스로 샘플링 되면 안 되는 경우가 있는데 특히 event-driven 시스템에서 그러하다. 발생가능한 파동 변화에 대응하기 위하여, 우리는 Equation 1을 고쳐서 샘플과 샘플 사이의 실제 time interval이 반영되도록 했다. 수용기가 있는 레지스터가 1차 로우패스 필터를 결정하는 전자회로를 직접 유추함으로써, \(\alpha\)는 sampling period \(T_e\)와 time constant \(\tau\)의 함수로 계산 가능하며, 두 변수는 초 단위를 갖는다(Equation 4). 레지스터와 수용기 신호값들은 time constant(\(\tau=RC\)) 및 그에 대응하는 회로 cutoff frequency \(f_c\)(Hz)를 결정한다(Equation 5).

 

Equation [4]

$$ \alpha=\frac{1}{1+\frac{\tau}{T_e}} $$

 

Equation [5]

$$ \tau=\frac{1}{2\pi f_c} $$ 

 

Equation [6]

$$ \hat{X}_i=(X_i+\frac{\tau}{T_e}\hat{X}_{i-1})\frac{1}{1+\frac{\tau}{T_e}} $$

 

Equation [7]

$$ f_c=f_{c_{min}}+\beta |\dot{\hat{X}}_i| $$

 

Sampling period \(T_e\) 또는 그 역수인 sampling rate는 타임스탬프로부터 자동으로 계산되므로, cutoff frequency \(f_c\)가 Equation 6에서 유일하게 조정가능한 파라미터가 된다. 여느 로우패스 필터와 같이, \(f_c\)를 감소시키면 jitter가 줄어드는 대신 lag이 증가한다. jitter-lag 사이에서 최선의 트레이드 오프를 찾아내는 것은 어려운 작업인데, 사람들은 움직임이 느릴 때는 jitter에 민감하게 반응하고, 움직임이 빠를 때는 lag에 민감하게 반응하기 때문이다. 바로 이것이 adaptive cutoff frequency가 필요하고 또 잘 동작하는 이유다. jitter를 줄이기 위해 속도가 느릴 때는 낮은 \(f_c\)값이 사용되며, lag을 줄이기 위해서는 속도에 비례해서 \(f_c\)가 증가한다.

 

우리는 cutoff frequency \(f_c\)와 절대속도값이 단순 선형 관계를 이루고 있음을 발견했다(Equation 7). derivative \(\dot{\hat{X}}_i\)와 같은 속도는 sampling rate를 사용해서 raw 신호값으로부터 계산된 다음, 선택된 cutoff frequency에 따라 로우패스 필터링된다. 이를 통해 jitter로 인해 발생하는 high derivative bursts(미분값이 폭발하듯 증가하는 현상)를 방지할 수 있다. 우리의 원유로 필터 구현은 고정상수로 1 Hz를 사용하며, 조정가능한 파라미터를 오직 2개만 남겼다. Equation 7에서의 절편 \(f_{c_{min}}\) 그리고 기울기 \(\beta\) 두 개만 조정함으로써 노이즈 필터링이 가능하다. 알고리즘 상세 내용은 부록으로 첨부했다.

 

Tuning and Applications

인간 모션을 트래킹하면서 jitter-lag을 최소화하기 위해, 2개의 파라미터는 간단한 2단계 절차를 따라 세팅할 수 있다. 최초 \(beta\)는 0으로 세팅하고 \(f_{c_{min}}\)을 1 Hz와 같이 적당한 중간값으로 세팅한다. 그러면 바디 부분은 안정적으로 고정되거나 매우 느린 속도로 움직이게 된다. 반면 \(f_{c_{min}}\)은 이러한 느린 움직임이 지속되는 동안 jitter를 제거하고 적당한 수준의 lag을 보존하도록 조정된다. 그 다음, 바디 부분이 서로 다른 방향으로 빠르게 움직이게 되면 \(\beta\)값은 lag 최소화에 집중하며 증가된다. \(f_{c_{min}}\)과 \(\beta\)는 명확한 개념적 관계를 갖고 있음을 유념하자. 

 

• 만약 high speed lag이 문제라면 \(\beta\)를 더 높게 세팅하면 된다.
• 만약 slow speed jitter가 문제라면  \(f_{c_{min}}\)를 더 낮게 세팅하면 된다.

 

회전하는 입력값도 위와 유사한 튜닝 프로세스를 사용하지만, 회전축과 각도는 각각 별도로 필터링한다.

 

원유로 필터의 다른 용례로는 노이즈가 섞인 수치값들을 시각화하는 것인데, 그래픽 어플리케이션 퍼포먼스를 모니터할 때 불안정한 프레임 레이트가 사용되는 경우를 들 수 있다. 이 때 목표는 수치값들을 보기 편하게 jitter를 감소시키면서, 제때 수치값이 나타나도록 lag을 최소화하는 것이다. 튜닝은 휴먼 모션 트래킹과 유사하다. 수치 텍스트가 안정적으로 나타날 때까지 \(f_{c_{min}}\)를 조정한 다음, 안정성을 해치기 직전까지 \(\beta\)를 증가시켜 lag을 최소화하면 된다.

 

COMPARISON WITH OTHER FILTERS

원유로 필터를 다른 필터링 기법과 비교하기 위해, 우리는 시스템 커서의 XY 위치값을 주기적으로 샘플링하여 노이즈를 첨가한 다음 필터링된 커서 위치를 시각화하는 파이썬 어플리케이션을 만들었다. 각 필터는 인터랙티브하게 튜닝 가능하며, 모든 필터는 동시에 시각화하여 파라미터 세팅 및 필터 종류에 따른 jitter-lag 퍼포먼스를 비교할 수 있도록 했다. 튜닝이 완료된 후, 노이즈가 없는 버전과 첨가된 버전 그리고 모든 필터의 필터링 아웃풋의 시스템 커서 위치값을 타임스탬프에 따라 로그로 기록될 수 있도록 했다. 우리는 맥북프로 1440*900 (109 PPI) 디스플레이를 사용했다.

 

비교 작업에 있어서, 우리는 X, Y 좌표값에 대해 50dB SNR 독립 가우시안 화이트노이즈를 적용했다. 칼만 필터의 경우 공식 구현 코드를 사용했으며 그 외 moving average, single exponential, LaViola double exponential smoothing은 자체 구현했다. 우리는 moving average를 먼저 튜닝하고 베이스라인 퍼포먼스로 사용했다. moving average에서 직전 14개를 초과하는 데이터 값들을 사용할 경우 jitter가 더 이상 감소하지 않고 lag만 증가하는 것이 확인되었기에 \(n=14\)를 사용했다. 그 다음 우리는 moving average 베이스라인에 jitter reduction이 근접할 때까지 다른 필터를 튜닝한 뒤 lag을 감소시키는 방향으로 튜닝을 진행했다.

 

single exponential smoothing은 매우 낮은 알파 파라미터 \(\alpha=0.11\)일 때 베이스라인 jitter에 도달했다. 이를 통해 단일 파라미터만을 조정하는 방법은 상당히 어렵다는 것을 알 수 있다. LaViola의 double exponential smoothing 필터의 경우, 베이스라인 jitter reduction은 보다 더 낮은 알파 파라미터 \(\alpha=0.06\)에서 달성되었으며 lag 퍼포먼스가 향상되었다. 그러나 포인터 속도가 급격히 감소할 때 오버슈팅이 발생하는 문제가 생겼다. 칼만 필터의 경우, 우리는 measurement noise 공분산을 인위적으로 가한 가우시안 노이즈의 분산값(18.06)으로 세팅한 다음, 베이스라인 jitter reduction에 도달할 때까지 process noise를 조정했다(0.3). 이러한 세팅에서 발생한 lag은 moving average, single-exponential 필터와 유사한 수준이었다.

 

원유로 필터의 경우, 우리는 베이스라인 jitter reduction을 먼저 맞춘 다음에 상기 기술한 튜닝 절차에 따라 lag을 최적화했다. 1차 튜닝 단계에서 \(f_{c_{min}}=1 Hz\), \(\beta=0\) 세팅으로 베이스라인 jitter reduction을 달성했으며 lag은 single exponential smoothing과 유사한 수준이었다. 2차 튜닝 단계에서 \(\beta\)값을 0.007까지 증가시켰을 때 lag은 거의 인식불가능한 수준까지 억제된 반면 움직임이 정적이거나 느릴 때 베이스라인 jitter reduction을 유지할 수 있었다. 별첨한 비디오에서 우리가 원유로 필터 튜닝 프로세스 및 필터 퍼포먼스를 시연한 것을 확인할 수 있다.

 

수치적인 비교의 경우, 통상 데스크탑 사용 환경 하에 1시간 가량 시스템 커서의 위치를 60 Hz에서 기록했다. Figure 1은 4개의 스피드 인터벌에 따라서 각각의 필터링된 커서 위치와 실제 위치 간의 거리를 나타내고 있다. 각 필터의 튜닝은 움직임이 없을 때에 베이스라인 jitter reduction에 도달하도록 이루어졌으므로, 필터링된 커서 위치와 본래의 커서 위치 간의 에러는 주로 움직임이 발생하는 구간의 lag 때문에 발생한다는 점을 알아두자. 속도가 더 빨라질 수록, 필터링된 커서 위치에 더 큰 lag이 발생하며 따라서 실제 커서 위치와의 거리도 멀어지게 된다(0 mm/s 구간의 에러가 작은 이유는 오프셋이나 오버슈팅 때문일 가능성이 높다). 대체로 모든 필터는 유사한 수준의 lag을 나타냈지만 원유로 필터의 경우 모든 속도별 구간에서 더 낮은 lag을 기록했다.

 

 

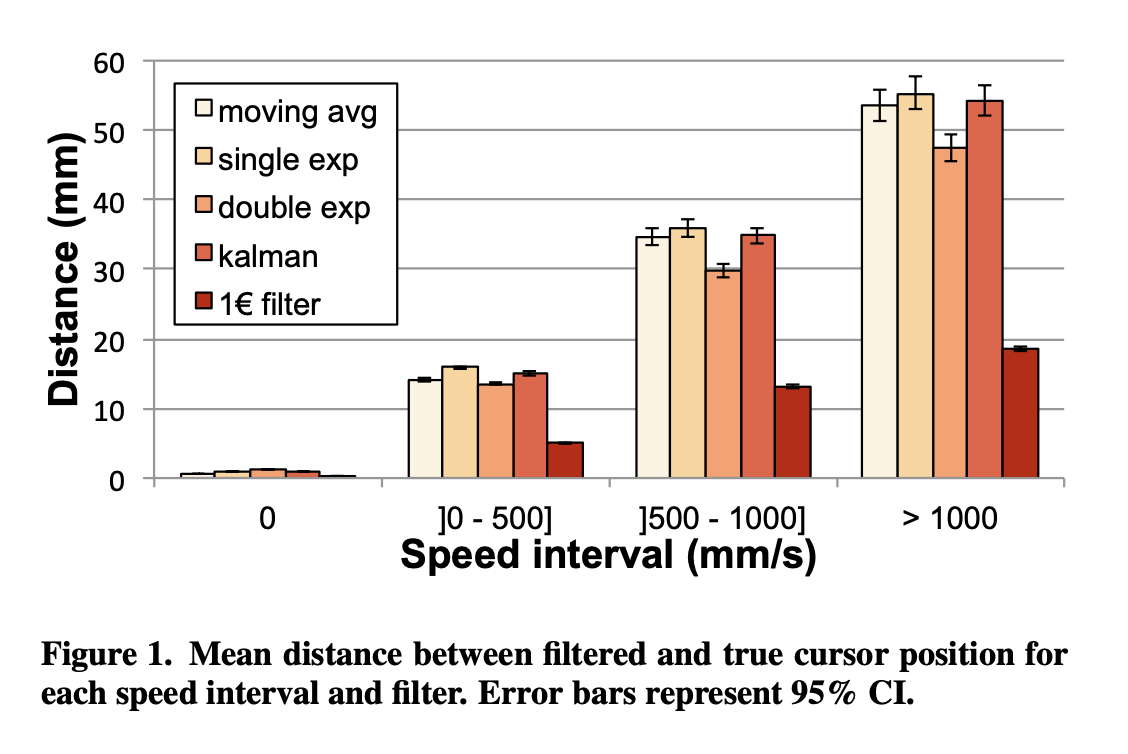
종합적인 비교를 위해 우리는 각 필터가 동일 데이터셋에 대해 갖는 Standard Error of the Mean (SEM)을 mm 단위로 계산했다. 원유로 필터가 가장 작은 SEM 0.004를 기록했고, 그 다음으로 LaViola의 double exponential smoothing이 0.013, moving average / Kalman Filter 0.015, single exponential smoothing 0.016 순이었다. 이러한 평가를 수행한 목적은 현실적인 조건 하에서 원유로 필터의 직관적인 성능을 보이기 위함이다. 우리는 추후 사용자 실험, 합성 레퍼런스 무브먼츠, 다양한 노이즈 세팅 그리고 "잡음이 많이 발생하는" 하드웨어 등 다양한 비교 실험을 진행할 예정이다.

 

CONCLUSION

더 이사아 HCI(Human-Computer Interaction) 연구자 및 실무자들은 moving average로 신호 잡음을 필터링할 필요가 없다. 거의 모든 경우에서, 그들은 저수준의 신호처리 이슈라거나 칼만 필터와 같이 어렵고 튜닝과 구현 난이도가 높은 복잡한 기술과 씨름할 필요도 없다. 원유로 필터는 이해하기 쉽고, 구현하기 쉬우며, jitter-lag 최소화 튜닝이 간편한 직관적이고 실용적인 대안이다. 무엇보다, 더 좋은 결과물을 얻을 수 있으니까 말이다.