컴퓨터그래픽스_라이팅(1)

고려대학교 정보대학 컴퓨터학과 2019년 1학기 <컴퓨터그래픽스> 9강 라이팅 (1)

강의영상 플레이리스트 [Link]

강의자료 [Link]

 

Books · media lab

---

컴퓨터그래픽스 라이팅 (1)

Keywords

• Phong model
• diffuse
• specular
• ambient
• emissive

 

Phong Lighting Model

Lighting, illumination -> 빛과 물체 간의 상호작용을 다루는 기술

* 가장 유명한 라이팅 기법 = Phong model

 

상업 게임에 널리 채택되었으며, 고급 라이팅 기법의 근간이 됨

* Phong model은 4개 항(term)으로 구성됨

• diffuse
• specular
• ambient
• emissive

 

Phong Lighting Model - Diffuse Term (난반사)

가장 단순하고 처리하기 쉬운 광원 = directional light source

-> 대표적으로 태양, 매우 강하고 씬에서 멀리 떨어져 있어서 모든 물체가 universal direction에서 빛을 받게 됨

(엄밀히 말하면 정확하게 같은 방향은 아니지만, 멀리 떨어져 있으므로 거의 모든 물체가 비슷한 방향에서 빛을 받음)

 

Phong model의 첫번째 - "난반사" (diffuse reflection)

* 우리는 빛으로부터 반사된 색상을 물체의 색상으로 인지한다.

* 빛을 받은 물체가 모든 방향에 대해 동일한 강도로 반사하는 이상적인 상태 = 난반사라고 한다.

* 따라서 눈(카메라) 위치와 상관없이 동일 물체로부터 동일한 양의 반사를 관측할 수 있다.

 

 

"그렇다면 광원에서 물체로 얼마나 강한 빛이 들어오는가"

* 입사각이 물체가 받는 빛의 양을 결정한다.

* 언제 빛의 양이 최대가 되는가? -> 광원이 표면 바로 위에 있을 때 (노말 방향에 위치할 때) -> \(\theta=0\)

* 언제 빛의 양이 최소가 되는가? -> 노말과 수직을 이루는 방향에서 빛이 들어올 때 -> \(\theta=90\)

* 입사각과 빛의 양은 반비례한다 -> 함수로 표현하면 \(cos \theta\)

 

앞서 살펴본 dot product 정의에 따라,

$$n\cdot l = ||n|| ||l|| cos \theta$$

* normal 크기는 1로 만드는 것이 원칙

* \(l\)도 크기를 1로 만들어보면? -> \(n \cdot l = cos \theta\)

* 즉, \(cos \theta\)는 \(p\)가 받는 빛의 양을 결정한다.

 

단, 물체가 받는 빛의 양은 음수가 될 수 없으므로, lower bound 0으로 제한한다.

$$max(n\cdot l, 0)$$

 

Phong Lighting Model - Diffuse Term (cont'd)

빛의 강도는 위와 같이 구했을 때, 그럼 어떤 "색상"이 되어야 하는가?

* RGB (1,1,1)인 백색광이 있을 때, 물체가 붉은색으로 나타난다면 R만 반사하고 G, B는 흡수했다는 의미

-> 머티리얼 파라미터를 통해 쉽게 필터링 구현 가능

-> \((1,1,1)\otimes (1,0,0)=(1,0,0)\)

*\(\otimes\) = component-wise multiplication

 

 

[Diffuse term]

$$max(n\cdot l, 0) s_d \otimes m_d$$

* \(s_d\) = source(light) for diffuse / \(m_d\) = material for diffuse

* \(m_d\)는 물체가 가진 고유의 색상을 의미하며, 일반적으로 텍스쳐가 \(m_d\) 값을 제공

 

Phong Lighting Model - Specular Term (정반사)

정반사 = 일정한 방향으로 들어오는 빛에 대해 특정 방향이나 그 중심으로만 반사가 되는 것

* 카메라가 어느 위치에 있는가가 최종 결과물에 영향을 미친다.

* 입사각에 대해 대응하는 반사각이 존재한다.

 

Specular term은 highlights (핀 조명)으로 물체 표면을 반짝이게 만드는 데 관여한다.

* light vector \(l\), view vector \(v\), reflection vector \(r\) 세 가지 벡터로 구성

* view vector = p에 대한 카메라의 방향

 

[Computing the reflection vector]

 

\(s\)에 대한 두가지 방정식을 얻은 뒤 \(r\)에 대해 정리하여, \(n\)과 \(l\)로 표현되는 관계식을 구할 수 있다.

 

$$s=n cos \theta - l$$

$$s=r-n cos \theta$$

$$ r=2n cos \theta - l $$

$$ \ \ \ = 2n(n \cdot l) - l $$ 

 

 

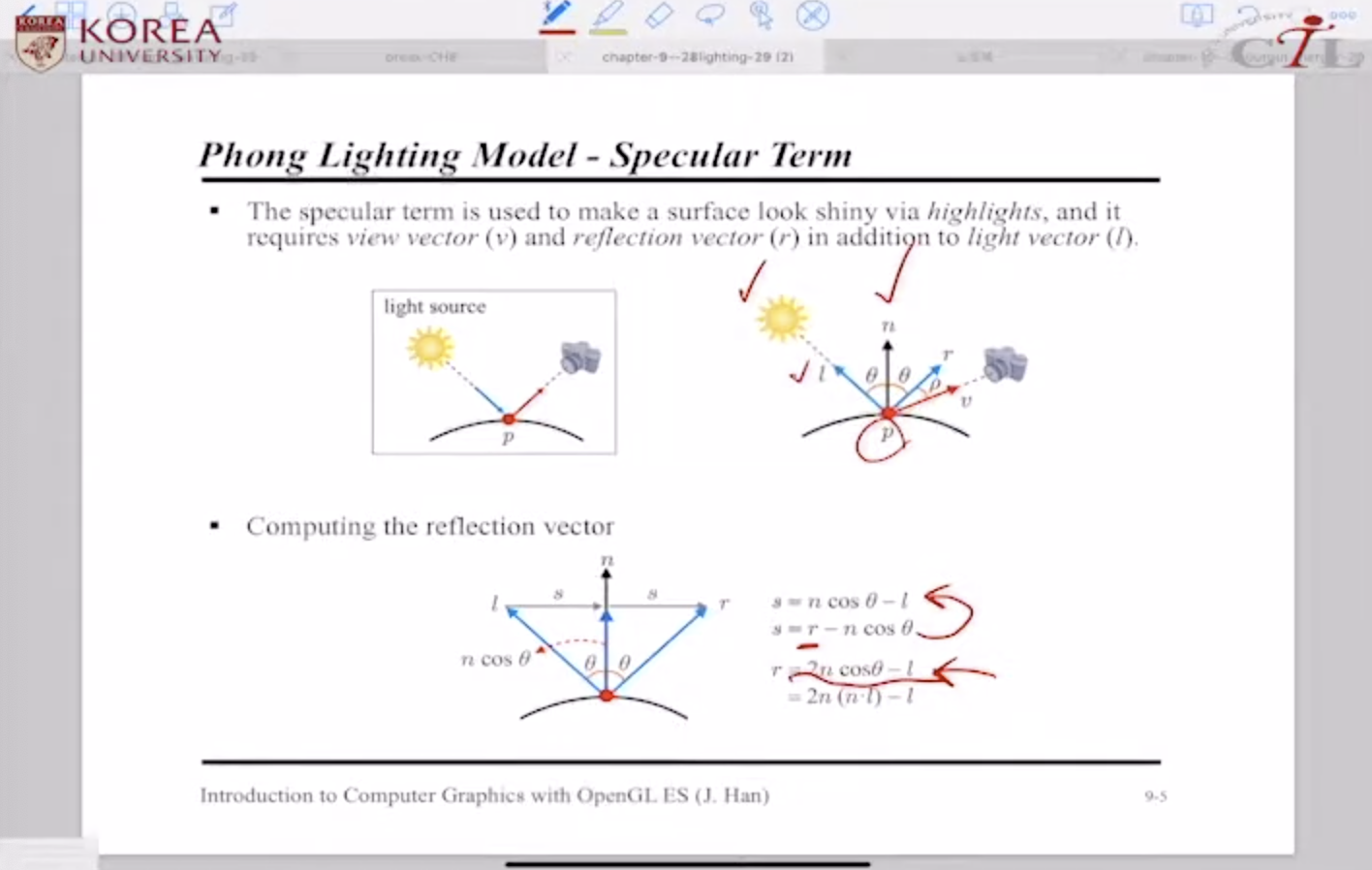
Phong Lighting Model - Specular Term (cont'd)

highly view-dependent (camera location is important)

\(\rho\) = reflection vector \(r\)와 view vector \(v\)가 이루는 사잇각

 

* 카메라가 정확히 반사각과 맞아 떨어지면 완벽한 shiny surface (\(\rho=0\))

* 완전하게 맞아 떨어지지 않는 경우 -> \(\rho=0\)일 때 가장 highlight 극대화되고, \(\rho\)가 증가함에 따라 급격하게 반사량 하락

* \(\rho\) 증가에 따른 highlight 감소는 \((r \cdot v)^{sh}\)로 보통 추정하며, \(sh\)는 물체 표면이 매끈한 정도를 의미함

 

[Specular term]

$$(max(r \cdot v, 0))^{sh} s_{s} \otimes m_{s}$$

 

* \(sh\) 지수를 통해 highlight 반비례 관계를 적용

* diffuse와 유사한 형태로 lower bound = 0

* 색상까지 고려하기 위하여 light source for specular \(s_s\), material for specular \(m_s\) 항을 추가

 

\(m_d\)는 RGB가 아닌 grayscale(r=g=b) 값!

* specular는 얼마나 물체 고유의 색깔을 죽일 것인가를 결정해야 하기 때문

* 광원의 색(ex. 백색광)을 그대로 내보내고 싶다 -> \(m_s = (1,1,1)\) 

* 10% 정도는 광원을 흡수하고 싶다 -> \(m_s = (.9, .9, .9)\)

 

 

Phong Lighting Model - Ambient and Emissive Terms

Ambient light -> 배경광, 주변광, 간접광, 물체에 간접적으로(약하게) 영향을 미치는 광원

* 물체에 대하여 빛이 온갖 방향으로 들어오고, 온갖 방향으로 반사됨

* 광원이 온갖 곳에 있다고 전제하므로 별도의 \(l\) 벡터를 필요로 하지 않으며, 온갖 방향으로 반사되므로 노말 벡터도 의미가 없어진다

* 따라서 아래와 같이 단순하게 표현 - 과학적으로 엄밀, 정교하게 구현하는 것은 아니지만 매우 작은 값으로 그럴듯하게 표현하는 것

 

[Ambient term]

$$s_a \otimes m_a$$

 

Emissive -> amount of light emitted by a surface itself

* 물체 표면이 자체적으로 발생시키는 고유의 빛을 의미함

* RGB 컬러인 \(m_e\) 만으로 표현, 통상적으로 매우 작은 값

 

[Emissive term]

$$m_e$$

 

 

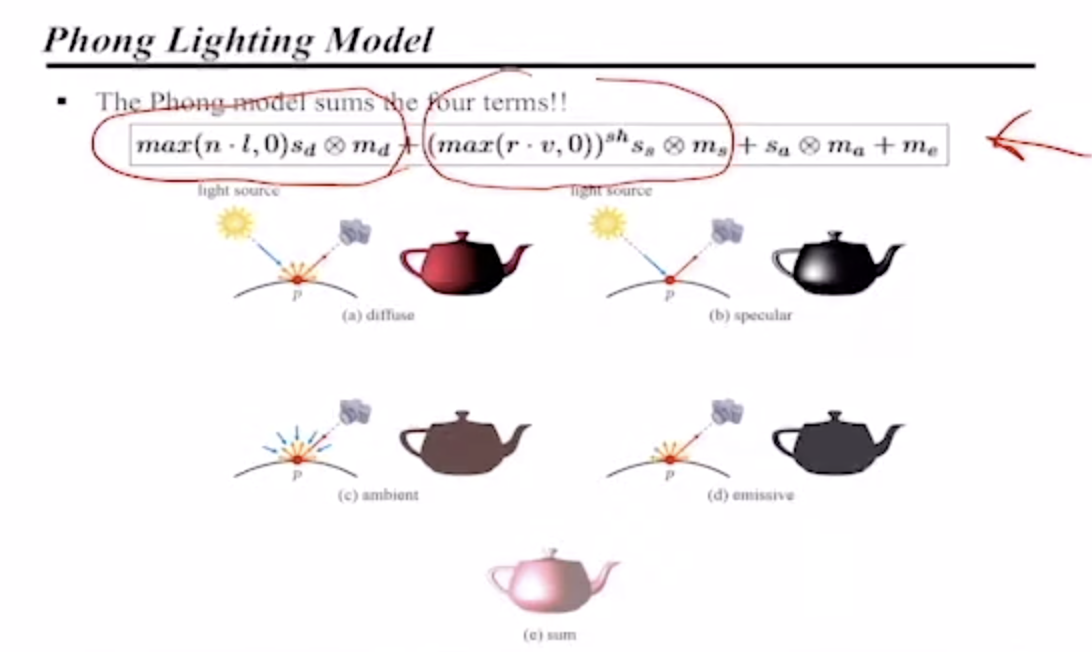
Phong Lighting Model

위의 4개항을 모두 더한 것 = Phong model!

 

[Phong model]

$$max(n \cdot l, 0)s_d \otimes m_d + (max(r \cdot v, 0))^{sh} s_s \otimes m_s + s_a \otimes m_a + m_e$$