티스토리 뷰
고려대학교 정보대학 컴퓨터학과
2019년 1학기 <컴퓨터그래픽스> 수학 기초
강의영상 플레이리스트
https://www.youtube.com/watch?v=774mc7tC594&list=PLYEC1V9tJOl03WLDoUEKbiYW_Xt4W6LTl&index=3
강의자료
https://media.korea.ac.kr/books/
Books · media lab
Introduction to Computer Graphics with OpenGL ES Review and Recommendations 이 책의 영문 제목 “Introduction to Computer Graphics”를 “A Painless Introduction to Computer Graphics”라는 닉네임으로 바꿔서 부르고 싶다. 수학을
media.korea.ac.kr
컴퓨터그래픽스 수학 기초
Keywords
- Orthonormal basis vs. Non-orthonormal basis
- Standard basis vs. Non-standard basis
- Dot product in 2D / 3D space
- Cross product in 3D space
- Line, Ray and Linear Interpolation
선형대수 기본개념


OpenGL -> 매트릭스-벡터 곱셈 연산에서 벡터가 매트릭스 우측에 놓이며 열벡터를 사용
Direct3D -> 매트릭스-벡터 곱셈 연산에서 벡터가 매트릭스 좌측에 놓이며 행벡터를 사용


좌표계와 기저 (Coordinate System and Basis) - 2차원 공간
좌표계는 원점 origin + 기저 basis로 구성된다
좌표계는 그래픽스에서 간단하게 공간 space라고 부른다
Orthogonal 기저 벡터 -> 서로 90도 사이각을 갖는 표준 기저 벡터
\(e_{1}(1,0)\), \(e_{2}(0,1)\) 두 벡터의 선형조합으로 2차원 공간에서 가능한 모든 벡터 표현 가능
Orthonormal = Orthogonal + Normalized
\(e_{1}(1,0)\), \(e_{2}(0,1)\) 두 벡터는 단위벡터이며, 단위벡터를 만드는 과정을 normalization 이라고 부름
Non-orthonormal / Non-standard -> 서로 90도가 아닌 사이각을 갖는 비표준 기저 벡터
\(e_{1}(1,1)\), \(e_{2}(0,2)\)
Orthonormal but non-standard?
서로 90도 사이각을 갖고 단위벡터이지만 표준은 아닌 경우
\(u(\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}})\), \(v(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})\)

좌표계와 기저 (Coordinate System and Basis) - 3차원 공간
3차원 Orthonormal / standard basis
\(\{e_1, e_2, e_3\}, where \ e_1=(1,0,0), e_2=(0,1,0), e_3=(0,0,1)\)
*물론 3차원 공간에서도 non-standard orthonormal 기저가 존재함
*이후 강의에서 소개될 모든 2D / 3D 기저는 모두 orthonormal로 국한함

Dot Product (Inner Product, 내적) - 2D & 3D
대수적인 정의 & 기하학적인 정의
- 두 개의 벡터가 수직을 이룬다면 길이와 상관없이 dot product = 0
- 두 개의 벡터가 예각을 이룬다면 dot product > 0
- 두 개의 벡터가 둔각을 이룬다면 dot product < 0

2D orthonormal non-standard
\(u(\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}})\), \(v(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})\)
- u-u, v-v 내적은 1
- uv 내적은 0

Cross Product - 3D only
a, b 크로스 프로덕트 벡터는 두 벡터가 이루는 평행사변형의 면적과 같다.
a, a 크로스 프로덕트 결과는 (0, 0, 0)이며 blad zero 0으로 표현한다.
a, b 크로스 프로덕트는 b, a 크로스 프로덕트와 방향이 반대이고 길이는 동일하다.

https://en.wikipedia.org/wiki/Cross_product
Cross product - Wikipedia
From Wikipedia, the free encyclopedia Jump to navigation Jump to search Mathematical operation on vectors in 3D space In mathematics, the cross product or vector product (occasionally directed area product, to emphasize its geometric significance) is a bin
en.wikipedia.org
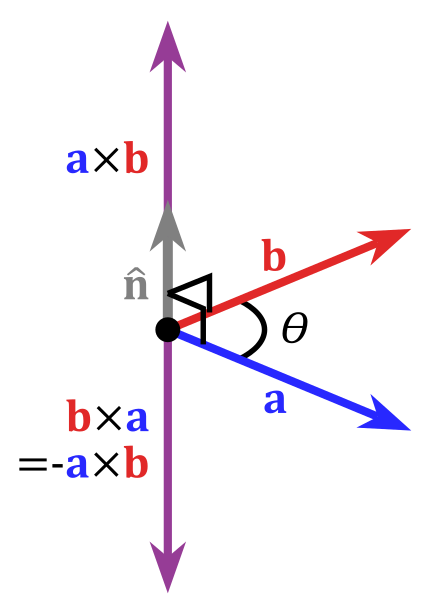
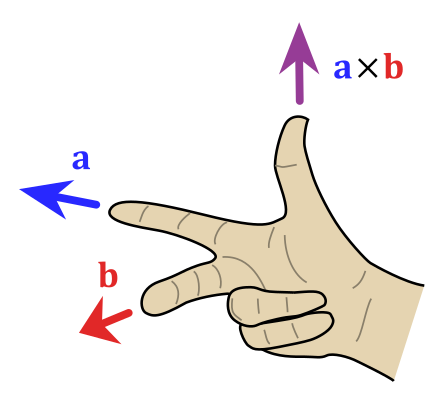
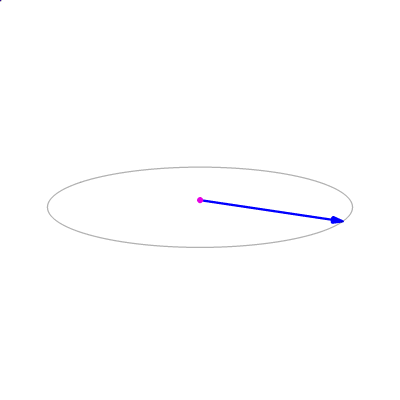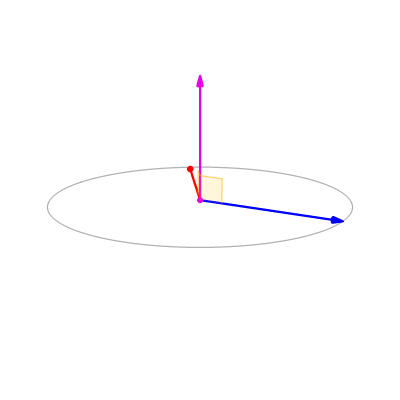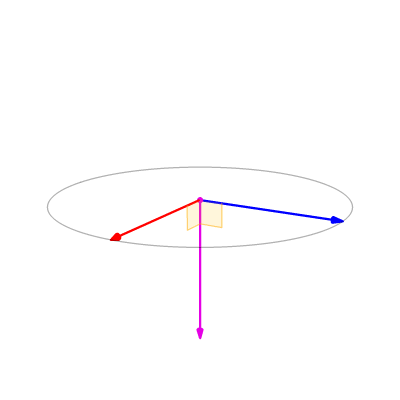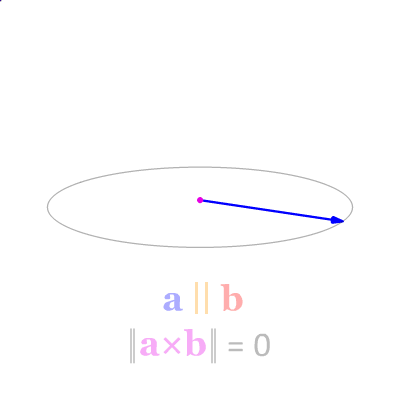
- 두 벡터 a, b가 평행(나란함) -> 두 벡터의 외적은 0
- a, b가 수직 -> \(sin\theta\)가 가장 커짐 -> 길이 최대화
방향과 길이는 알 수 있다, 그러나 \(a\ \text{x} \ b\)의 3차원 좌표는 어떻게 구할까?
엄밀한 정의는 교재에 수록 [Note: Derivation of cross product]

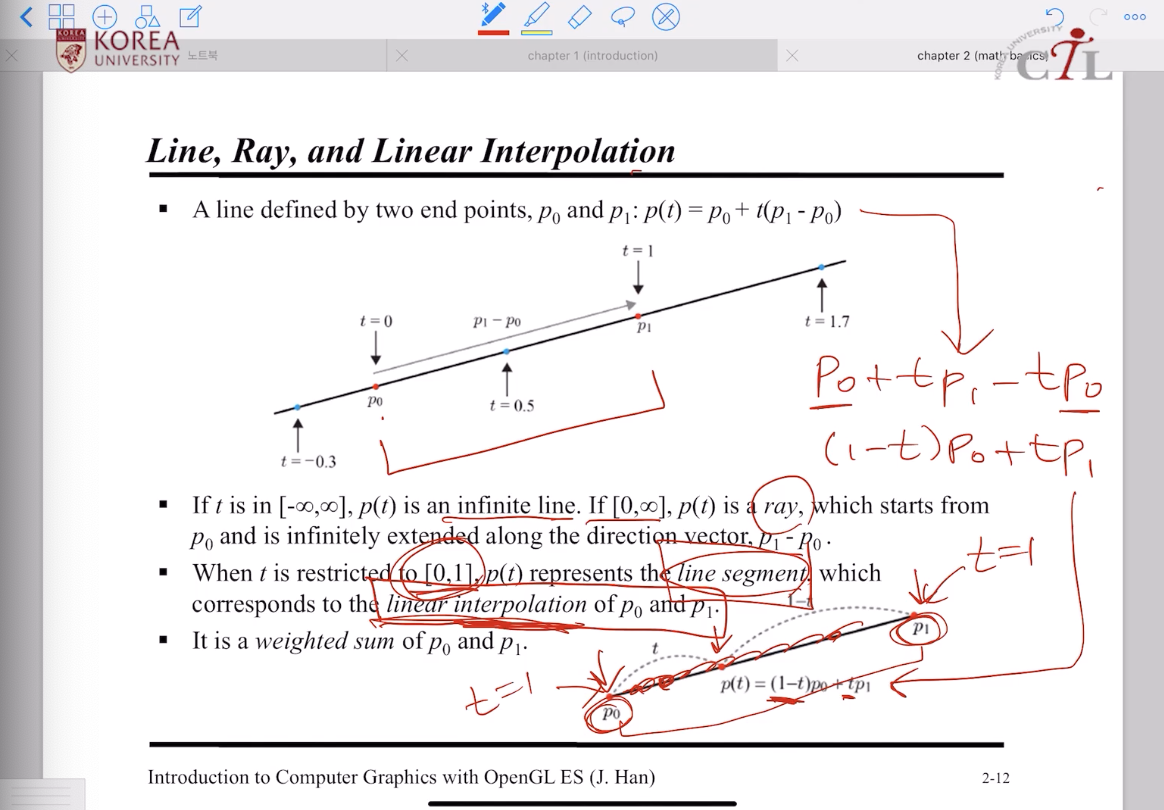
Line, Ray, and Linear Interpolation
두 점 사이를 잇는 무한한 길이의 직선의 모든 점을 표현하기

Linear Interpolation 선형보간은 그래픽스에서 매우 폭넓게 활용되는 중요한 개념!
시작점과 끝점 사이에 있는 모든 점은 양쪽 끝점을 선형보간하여 만들어낼 수 있다.
Linear interpolation in 3D space
선형보간된 점의 3차원 좌표값 계산, 2차원과 동일한 보간 공식을 적용
RGB 데이터에 대한 선형보간 예시

'3D Computer Graphics > Learnings' 카테고리의 다른 글
| 컴퓨터그래픽스_좌표계와 변환(3) (0) | 2022.04.23 |
|---|---|
| 컴퓨터그래픽스_좌표계와 변환(2) (0) | 2022.04.22 |
| 컴퓨터그래픽스_좌표계와 변환(1) (0) | 2022.04.21 |
| 컴퓨터그래픽스_모델링 (0) | 2022.04.15 |
| 컴퓨터그래픽스_서론 (0) | 2022.04.15 |
- Total
- Today
- Yesterday
- PoseNet
- tensorflow.js
- 메타버스
- vertex shader
- 고려대학교 한정현
- 컴퓨터그래픽스 좌표계와 변환
- 컴퓨터그래픽스
- 3d affine transform
- 원유로필터
- 컴퓨터그래픽스 강의
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
