티스토리 뷰
고려대학교 정보대학 컴퓨터학과 2019년 1학기 <컴퓨터그래픽스> 4강 좌표계와 변환(1)
강의영상 플레이리스트 [Link]
강의자료 [Link]
Books · media lab
Introduction to Computer Graphics with OpenGL ES Review and Recommendations 이 책의 영문 제목 “Introduction to Computer Graphics”를 “A Painless Introduction to Computer Graphics”라는 닉네임으로 바꿔서 부르고 싶다. 수학을
media.korea.ac.kr
컴퓨터그래픽스 좌표계와 변환 (1)
Keywords
- Affine transform
- Linear transform
- Scaling \(S\)
- Rotation \( R \)
- Origin vs. Arbitrary point
- and many others
- Translation \(T\)
- Cartesian coordinates
- Homogeneous coordinates
- Linear transform
Scaling
Scaling = 벡터의 축소와 확대
그래픽스에서는 축소확대를 scaling factor 행렬에 대한 행렬곱으로 표현하고 연산함

Rotation
회전변환 또한 축소확대와 동일하게 행렬곱으로 정리하여 표현, 연산 가능하다

회전변환이라 함은 "반시계 (counter-clockwise)" by default
시계 정방향의 경우 마이너스 파라미터를 적용

Translation and Homogeneous Coordinates
Translation 이동변환 / Homogeneous coordinates 동차좌표
축소확대 및 회전 변환과 달리 벡터합으로 표현되고 연산한다
동차좌표(homogeneous coordinates) 이용하면 행렬곱으로도 표현, 연산 가능 (축소확대, 회전변환과의 통일성 위해)
$$ (x,y) \rightarrow (x,y,1) $$
Translation matrix = Identity matrix의 3열에 \(d_x, d_y\) 삽입한다
\begin{equation*}
A =
\begin{pmatrix}
1 & 0 & d_x \\
0 & 1 & d_y \\
0 & 0 & 1
\end{pmatrix}
\end{equation*}

동차좌표의 3번째 좌표 \(w\) - 반드시 1이어야 할 필요는 없다, non-zero이면 임의의 값 가능함
[Cartesian coordinates -> Homogeneous coordinates]

[Homogeneous coordinates -> Cartesian coordinates]
\(w\) 값으로 동차좌표를 나눠주면 \(w=1\)인 평면으로 projection 됨
-> \(w\) 버리고 \(\frac{X}{w},\frac{Y}{w}\) 만을 취한다

하지만 여전히 통일성에 문제가 있다! -> 축소확대, 회전변환은 2x2 행렬로 표현하지만 동차좌표는 3x3?
축소확대, 회전변환 행렬도 3x3 꼴로 만들어준다.

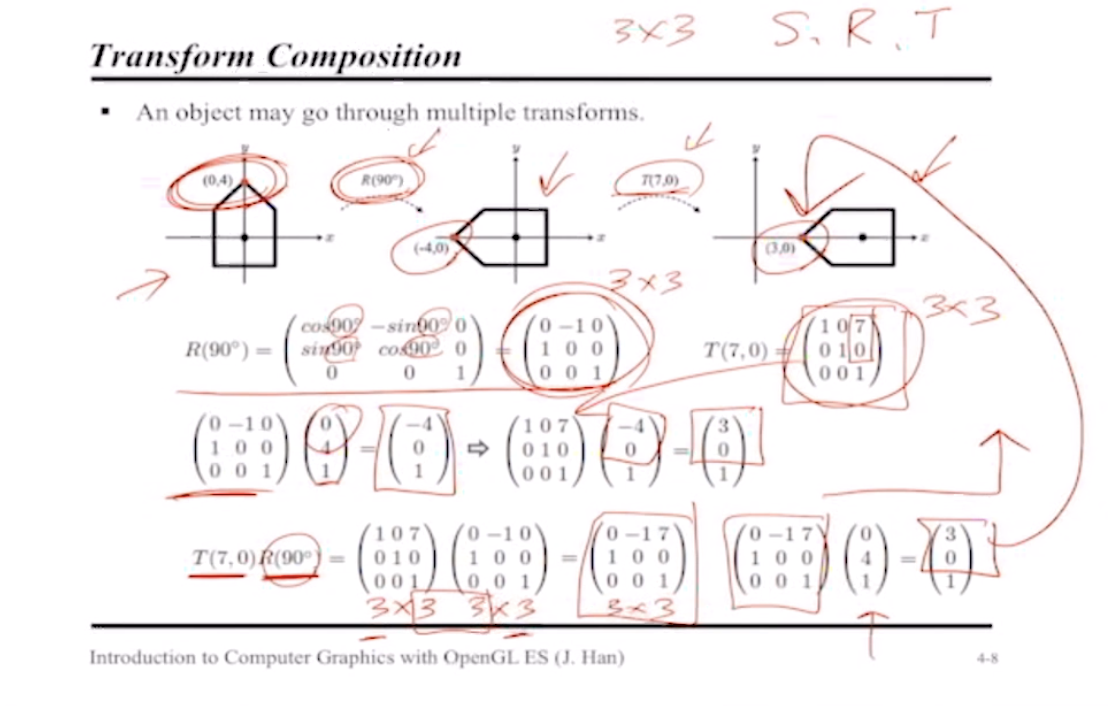
Transform Composition
오브젝트의 변환은 축소확대, 회전, 이동변환 등 여러 개의 변환들로 구성될 수 있다.
-> 변환의 종류와 상관없이 3x3 행렬로 표현 가능하므로 하나로 합쳐서 연산하는 것이 가능하다.
-> 단, 변환의 순서에 유의하여 연산을 수행할 것!
-> 변환행렬과 원행렬 간에 교환법칙은 성립하지 않는다

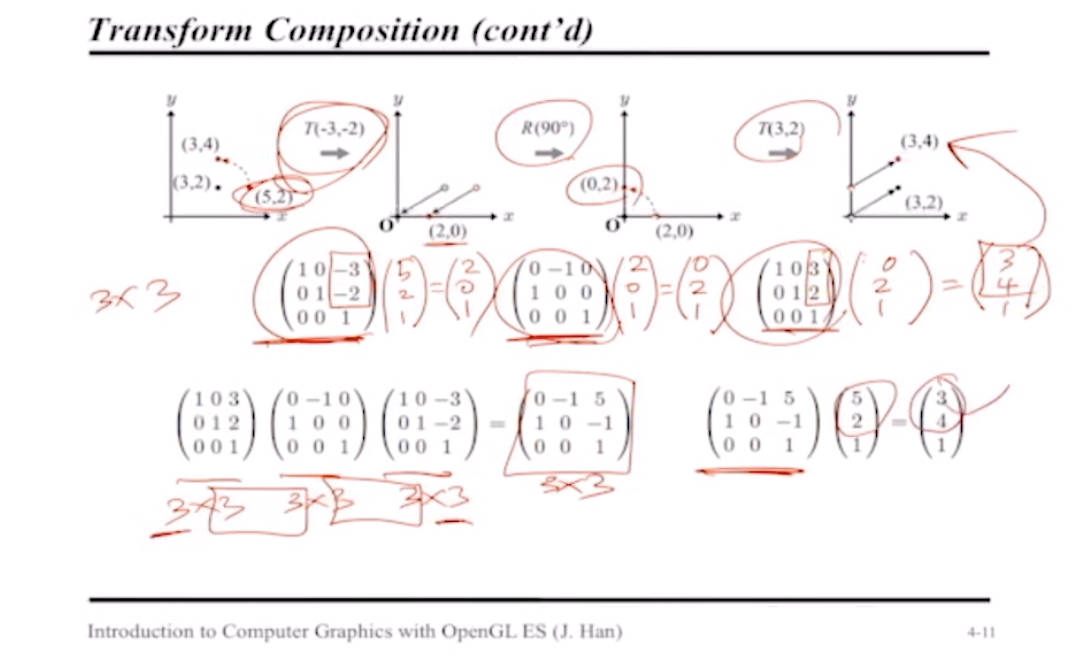
위에서 다룬 회전변환은 "원점(origin)을 중심으로 한 회전"에 대한 연산
원점이 아니라 임의의 한 점을 기준으로 회전시키는 방법은?
-> 임의의 한 점을 원점으로 이동 translation
-> 동일 translation을 원좌표에 대해서도 적용
-> rotation 연산
-> reverse translation, 제자리로 돌려놓기

[임의의 한 점에 대한 rotation 예시]
마찬가지로 transform composition으로 변환행렬 하나로 묶어서 연산할 수 있음
'3D Computer Graphics > Learnings' 카테고리의 다른 글
| 컴퓨터그래픽스_좌표계와 변환(3) (0) | 2022.04.23 |
|---|---|
| 컴퓨터그래픽스_좌표계와 변환(2) (0) | 2022.04.22 |
| 컴퓨터그래픽스_모델링 (0) | 2022.04.15 |
| 컴퓨터그래픽스_수학 기초 (0) | 2022.04.15 |
| 컴퓨터그래픽스_서론 (0) | 2022.04.15 |
- Total
- Today
- Yesterday
- tensorflow.js
- 고려대학교 한정현
- 컴퓨터그래픽스 좌표계와 변환
- 컴퓨터그래픽스
- 3d affine transform
- PoseNet
- vertex shader
- 원유로필터
- 메타버스
- 컴퓨터그래픽스 강의
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
