티스토리 뷰
고려대학교 정보대학 컴퓨터학과 2019년 1학기 <컴퓨터그래픽스> 5강 정점 처리(2)
강의영상 플레이리스트 [Link]
강의자료 [Link]
Books · media lab
Introduction to Computer Graphics with OpenGL ES Review and Recommendations 이 책의 영문 제목 “Introduction to Computer Graphics”를 “A Painless Introduction to Computer Graphics”라는 닉네임으로 바꿔서 부르고 싶다. 수학을
media.korea.ac.kr
컴퓨터그래픽스 정점 처리(2) - Vertex Processing
Keywords
- RHS vs. LHS
- z-negation
- cam external parameter vs. cam internal parameter
- fovy / aspect / n / f
- clip space & GPU clipping
- view frustum
- projection transform
- GPU rasterization requirement - LHS
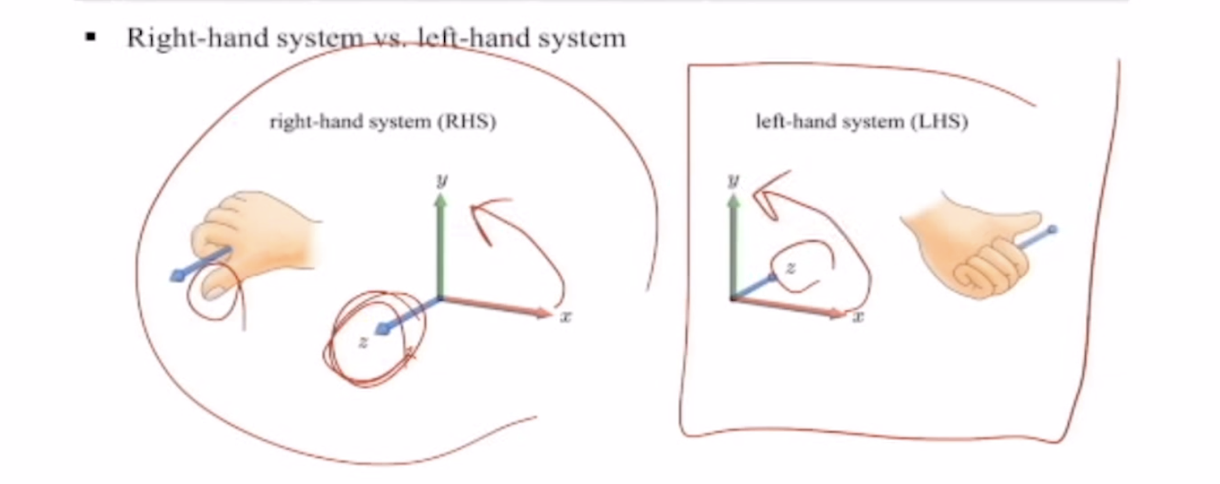
Right-hand System vs. Left-hand System
Vertex shader가 수행하는 3가지 변환 중 마지막 변환? (이전 포스팅 - world transform, view transform)
먼저 짚고 넘어가야 할 것 -> 오른손 좌표계(RHS) vs. 왼손 좌표계(LHS)
오른손 좌표계가 보편적으로 채택되고 있지만, 왼손 좌표계를 표준으로 하는 시스템도 존재하기 때문에 알아두어야 함.
(예) Direct3D는 왼손좌표계, OpenGL 오른손좌표계
E = \(\mathbf{EYE}\)
A = \(\mathbf{AT}\)
U = \(\mathbf{UP}\)
RHS 좌표계 정보를 그대로 가져와서 translation만 수행할 경우 비디오 렌더링 결과가 다르다 (좌우대칭)

RHS-LHS porting 솔루션은 너무나 간단하다!
* 정점(vertex) z좌표 부호만 바꿔주면 OK
$$\mathbf{EYE}_z \rightarrow -\mathbf{EYE}_z$$
$$\mathbf{AT}_z \rightarrow -\mathbf{AT}_z$$
$$\mathbf{UP}_z \rightarrow -\mathbf{UP}_z$$

View Frustum
Vertex shader의 world transform, view transform 이후 우리는 카메라 스페이스에 위치해 있음!
* 본 강의에서는 cam space 좌표계를 편의상 \(\{u,v,n\}\) 대신 \(\{x,y,z\}\) 으로 표현하기로 함
Camera external parameter vs. camera internal parameter
external : \(\mathbf{EYE}, \mathbf{AT}, \mathbf{UP}\)
internal : 렌즈 및 줌인 줌아웃 관련 파라미터
* fovy = field of view along y-axis = y축 방향으로(vertical, 상하) 얼마나 많은 시야각을 표현할 것인가
* apsect = \(\frac{w}{h}\) = \(\frac{width}{height}\) = horizontal, 수평 종횡비 ex) 16:9
fovy + aspect가 있으면 우리는 (z축을 따라) 무한한 크기의 origin을 꼭지점으로 갖는 피라미드를 만들 수 있다.

하지만 z축을 따라 무한하게 길어지는 피라미드는 너무 크다, 카메라 시야를 제한하자
-> \(n\) = near plane, 시야가 시작되는 지점
-> \(f\) = far plane, 시야가 끝나는 지점
-> \(n, f\)를 통해 잘려진 카메라 피라미드 = truncated pyramid = view frustum

주전자 손잡이 일부가 view frustum에 포함되지 않는다면? -> clipping by GPU
* 하지만 쉽지 않은 연산 처리, 깔끔하게 떨어지지 않는 경우가 많기 때문
* solution?

Projection Transform
주전자를 포함한 절도체(truncated pyramid)를 정육면체로 변환해 본다면 어떨까?
* 카메라 공간에서 정의된 frustum에서 잘린 부분을 그대로 처리하는 것은 어렵다
* 그렇다면 frustum을 정육면체로 변환해서 잘린 오브젝트를 처리하자 = projection transform
$$camera \ space \rightarrow projection \ transform \rightarrow clip \ space$$

절도체를 정육면체로 transform 한다는 것의 직관적 이해:
-> 원근법에 의해 서로 다른 길이를 갖는 \(l_1, l_2\) 선분 길이가 동일해진다.

Projection transform의 연산은 꽤 복잡한 편! - 본 강의에서는 상세한 유도과정 다루지 않을 것
* 단, 변환 행렬을 구성하는 항을 보면 초기에 세팅했던 파라미터 4종류로 구성되어 있음을 알 수 있다

- \(fovy\)
- \(aspect\)
- \(f\)
- \(n\)
시각화 애니메이션
"핵심은 주전자 오브젝트가 어떻게 변화하는가, view frustum 자체는 부수적인 것"
view transform (translation +rotation) -> 강체변환 (rigid motion), 물체 외형 변화X
projection transform -> NOT rigid motion, 물체 외형 변화 O, 축소확대를 포함하는 복잡한 비강제변환

여기까지 vertex shader 파트를 모두 다루었음 -> ~clip space
[Rasterizer]
* 하드웨어가 고정된 작업을 수행하는 파트
* 기존 GPU는 clip space가 왼손좌표계를 따를 것이라고 기대함
* 소프트웨어 파트인 vertex shader 코드를 수정해야 함 (RHS -> LHS) : z-negation
어차피 z-negation 필요하다면,
projection transform 변환행렬 자체를 바꿔서 한번에 연산하면 되지 않을까?
-> 4x4 행렬에서 3행을 모두 negation 해주면 간단! (이하 슬라이드 2번째 projection transform matrix에 반영)

여기까지, 최종 RHS-LHS 변환까지 vertex shader가 수행해야 할 일을 모두 다루었음!

- RHS vs. LHS
- z-negation
- cam external parameter vs. cam internal parameter
- fovy / aspect / n / f
- clip space & GPU clipping
- view frustum
- projection transform
- GPU rasterization requirement - LHS
'3D Computer Graphics > Learnings' 카테고리의 다른 글
| 컴퓨터그래픽스_래스터라이저(1) (0) | 2022.04.27 |
|---|---|
| 컴퓨터그래픽스_OpenGL ES와 셰이더 (0) | 2022.04.26 |
| 컴퓨터그래픽스_정점 처리(1) (0) | 2022.04.25 |
| 컴퓨터그래픽스_좌표계와 변환(3) (0) | 2022.04.23 |
| 컴퓨터그래픽스_좌표계와 변환(2) (0) | 2022.04.22 |
- Total
- Today
- Yesterday
- 원유로필터
- 컴퓨터그래픽스 강의
- tensorflow.js
- PoseNet
- 3d affine transform
- 컴퓨터그래픽스
- 메타버스
- 컴퓨터그래픽스 좌표계와 변환
- 고려대학교 한정현
- vertex shader
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
