티스토리 뷰
고려대학교 정보대학 컴퓨터학과 2019년 1학기 <컴퓨터그래픽스> 5강 정점 처리(1)
강의영상 플레이리스트 [Link]
강의자료 [Link]
Books · media lab
Introduction to Computer Graphics with OpenGL ES Review and Recommendations 이 책의 영문 제목 “Introduction to Computer Graphics”를 “A Painless Introduction to Computer Graphics”라는 닉네임으로 바꿔서 부르고 싶다. 수학을
media.korea.ac.kr
컴퓨터그래픽스 정점 처리(1) - Vertex Processing
Keywords
- GPU Rendering Pipeline
- Vertex Shader
- Rasterization
- Fragment Shader
- Output Merger
- World transform
- View transform
- Camera pose = position + orientation :
- Camera space
- Space change
- Origin Translation
- Basis Change
GPU Rendering Pipeline

* 셰이더(shader) = '프로그램(program)'의 동의어
* 렌더링 파이프라인은 개별 작성되어야 할 vertex shader, fragment shader와 함께, 고정된 함수 기능을 수행하는 rasterizeer, output merger가 포함됨
Vertex shader
* Vertex array에 저장된 입력 vertex 모두에 대하여 다양한 operation을 수행하는 프로그램
** Vertex = mesh vertex, 곡면(smooth surface)을 샘플링한 꼭지점(point)
*** Vertex array = 폴리곤 메쉬의 정보를 수치 형태로 컴퓨터 메모리에 저장하기 위한 데이터 포맷
컴퓨터그래픽스_모델링
고려대학교 정보대학 컴퓨터학과 2019년 1학기 <컴퓨터그래픽스> 모델링 강의영상 플레이리스트 https://www.youtube.com/watch?v=774mc7tC594&list=PLYEC1V9tJOl03WLDoUEKbiYW_Xt4W6LTl&index=3 강의자료 https:/..
dancefirst.tistory.com
Rasterizer
* Vertices로부터 삼각형을 모두 모아서 각 삼각형을 fragments라는 단위로 변환
* fragment는 각 삼각형이 갖는 화면 상의 픽셀 위치(pixel location of the triangle on the screen)로 정의되며, 색상을 결정하기 위한 데이터셋을 참고함
Fragment shader
* fragment color 계산
Output merger
* 최종적으로 픽셀 색상을 결정하기 위하여 fragment color를 사용, 취합
Vertex shader 핵심 = 일련의 vertex 변환작업 수행 (world transform, view transform, projection transform)
*[object space] -> world transform -> [world space] -> view transform -> [camera space] -> projection transform -> [clip space]

(what is world transform?)
컴퓨터그래픽스_좌표계와 변환(2)
고려대학교 정보대학 컴퓨터학과 2019년 1학기 <컴퓨터그래픽스> 4강 좌표계와 변환(2) 강의영상 플레이리스트 [Link] 강의자료 [Link] Books · media lab Introduction to Computer Graphics with OpenGL ES Rev..
dancefirst.tistory.com
World Transform (Revisited)
* world transform은 vertex array에 저장 기록된 vertex poistion에 대해 수행, 그렇다면 vertex normal은?
* world transform이
*
*
만약
* 평면이 향하는 방향의 각도가 틀어짐 -> NOT orthogonal (자기 자신과의 내적 != 1)
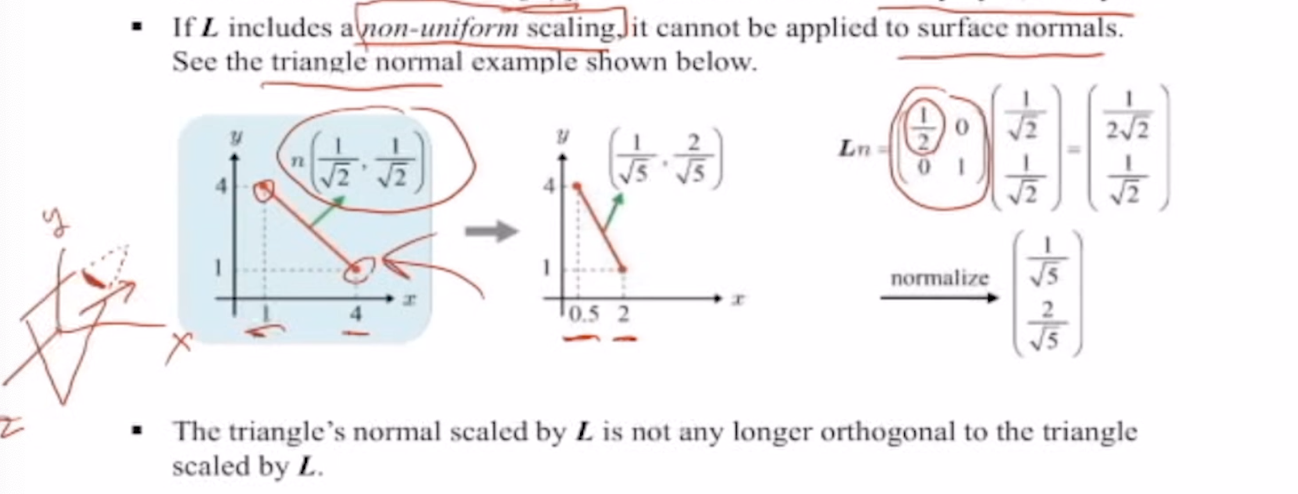
non-uniform scaling이 적용되었을 때,

*
* 그러나
* 따라서 우리는
* 정점 노말(vertex normal)은
*
View Transform
* Camera pose = position + orientation
* Camera space =
*
컴퓨터그래픽스_좌표계와 변환(3)
고려대학교 정보대학 컴퓨터학과 2019년 1학기 <컴퓨터그래픽스> 4강 좌표계와 변환(3) 강의영상 플레이리스트 [Link] 강의자료 [Link] Books · media lab Introduction to Computer Graphics with OpenGL ES Rev..
dancefirst.tistory.com
Camera 정보를 기반으로 공간을 구성하는 축을 재정의(변환) = space change (from world to camera)
Initially object space = world space =

"World-space objects can be newly defined in terms of the camera space in the manner of the teapot's mouth end -> EASIER TO CALCULATE"

Let's set
* Space change described intuitively: superimposing
* 첫번째로 수행할 작업은
* scene object와 camera space를 연결하는 보이지 않는 가상의 직선축을 생각해 보자 (이미지 점선)

Space change (tranlsation)을 통해서 world space와 camera space는 동일한 origin을 갖게 된 상태
* 두번째로 basis change 수행 :
world space - camera space를 동일 origin으로 맞춰 주었으므로, 변환된 object의 world space position은 camera space position과 동일하다고 생각할 수 있다.
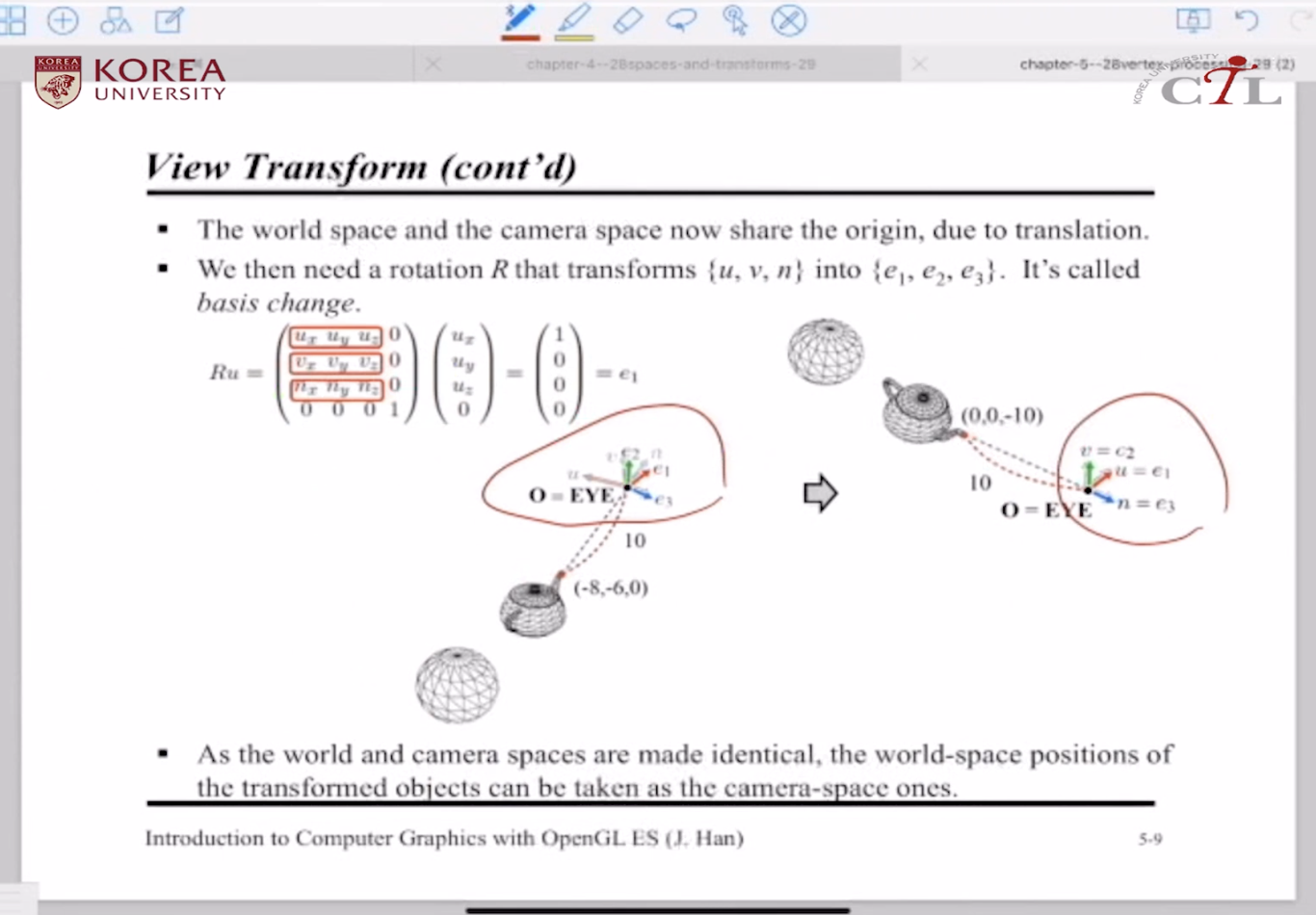
basis change에서 사용된 변환행렬의 형태와 관련 : 이전 학습했던 역 회전변환 참고 (=되돌린다)!

View Transform
공간이전(space change)은 translation과 rotation(basis change)의 조합으로 구성되며, 계속적으로 언급될 매우 중요한 개념. 특히, 3D 그래픽스 뿐 아니라 computer vision, robotics, AR/VR 분야에서도 space change는 매우 중요하다.
3차원을 다루는 모든 공학분야에서 space change는 매우 중요함!!

Space change (origin translation,
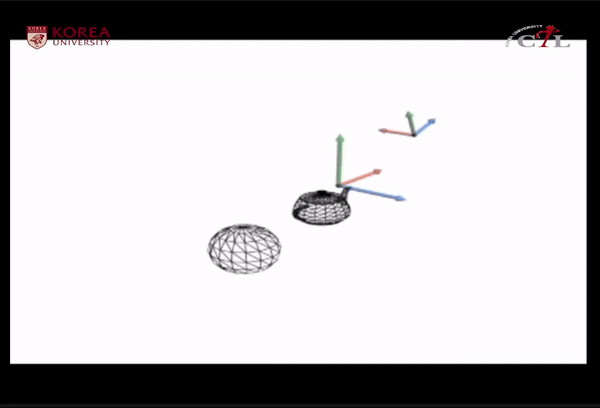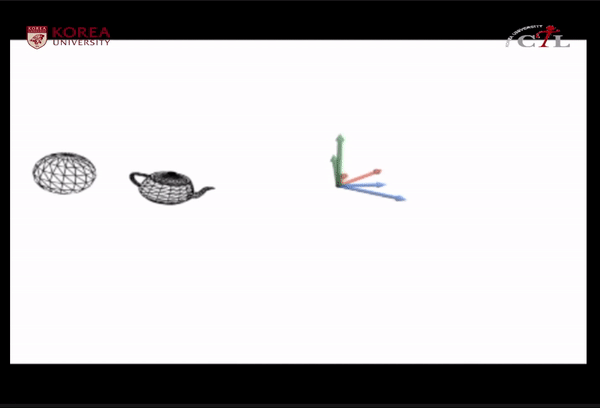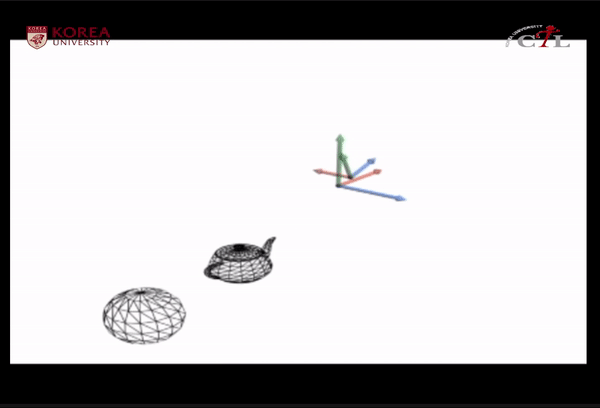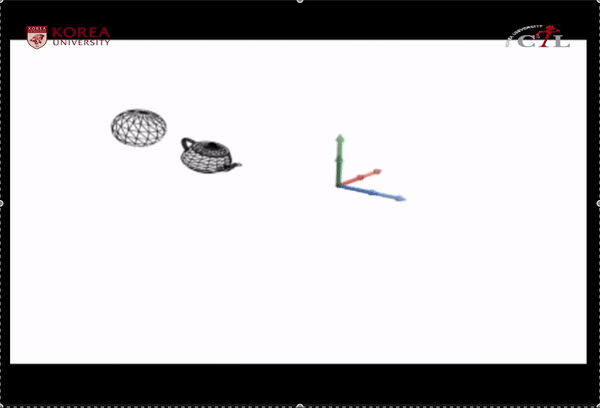
'3D Computer Graphics > Learnings' 카테고리의 다른 글
| 컴퓨터그래픽스_OpenGL ES와 셰이더 (0) | 2022.04.26 |
|---|---|
| 컴퓨터그래픽스_정점 처리(2) (0) | 2022.04.26 |
| 컴퓨터그래픽스_좌표계와 변환(3) (0) | 2022.04.23 |
| 컴퓨터그래픽스_좌표계와 변환(2) (0) | 2022.04.22 |
| 컴퓨터그래픽스_좌표계와 변환(1) (0) | 2022.04.21 |
- Total
- Today
- Yesterday
- tensorflow.js
- 컴퓨터그래픽스 좌표계와 변환
- 3d affine transform
- 컴퓨터그래픽스
- 원유로필터
- PoseNet
- 메타버스
- 컴퓨터그래픽스 강의
- 고려대학교 한정현
- vertex shader
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
