티스토리 뷰
고려대학교 정보대학 컴퓨터학과 2019년 1학기 <컴퓨터그래픽스> 4강 좌표계와 변환(2)
강의영상 플레이리스트 [Link]
강의자료 [Link]
Books · media lab
Introduction to Computer Graphics with OpenGL ES Review and Recommendations 이 책의 영문 제목 “Introduction to Computer Graphics”를 “A Painless Introduction to Computer Graphics”라는 닉네임으로 바꿔서 부르고 싶다. 수학을
media.korea.ac.kr
컴퓨터그래픽스 좌표계와 변환 (2)
Keywords
- Affine transform
- \([L|t]\)
- pose = position + orientation
- Rigid motion
- 3D scaling
- 3D rotation (CCW vs. CW rotations)
- 3D translation
- world transform
Affine Transform
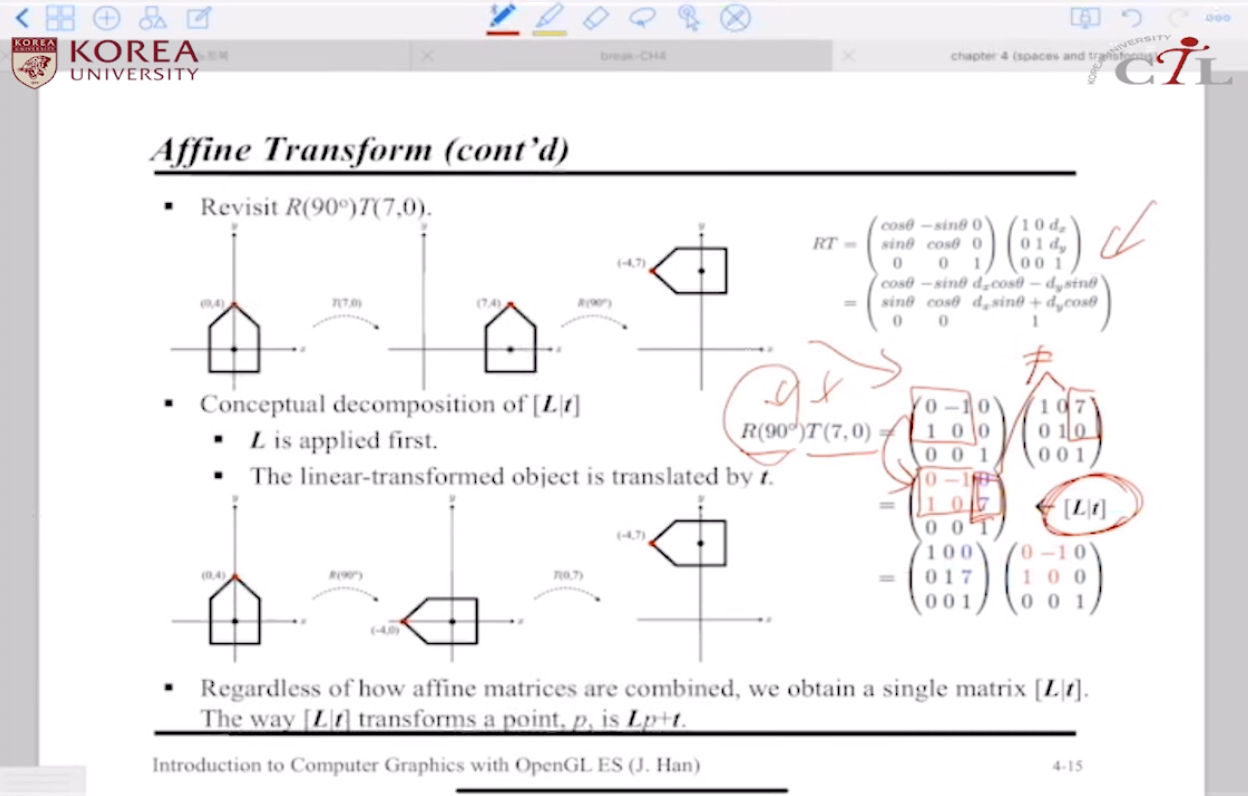
* When a series of affine transforms is concatenated to make a single 3x3 matrix, the third row is always \((0 \ 0 \ 1)\).
* 3x3 변환행렬을 몇 개를 적용하든, 변환연산 결과 affine matrix의 3행은 언제나 (0, 0, 1)이 된다. (homogeneous coordinate)
* affine matrix 3행을 무시하고, 나머지 2x3 행렬은 \([L|t]\)으로 표현하며, \(L\)은 앞부분 2x2 행렬, \(t\)는 3열부의 2차원 열벡터이다.
- \(L\)은 'combined' linear transform을 의미하며, 입력으로 받은 좌표가 포함되지 않는다
- \(t\)는 'combined' translation을 의미하며, 입력으로 받은 좌표의 선형변환 결과를 포함할 수 있다 (입력과 완전하게 동일한 경우는 일부의 특별한 경우)


conceptual decomposition of \([L|t]\)
* 선형변환을 먼저 적용한다
* \(t\)를 사용하여 translate 한다
* \([L|t]\)이 하나의 점을 변환하는 방식 -> \(Lp+t\)
Rigid Motion
강체 모션 = shape는 그대로 유지시키되, pose (position + orientation) 만을 바꾸는 변환
*단, scaling은 배제하므로 연산 결과는 \([R|t]\)로 표현한다.
- \(R\) = 'combined' rotation which does not include any translation terms
- \(t\) = 'combined' translation which usually includes the rotation terms
conceptual decomposition of \([R|t]\)
* 회전변환을 먼저 적용한다
* \(t\)를 사용하여 translate 한다
* \([R|t]\)이 하나의 점을 변환하는 방식 -> \(Rp+t\)
일반적으로 스케일링을 배제한 affine transform이 더 자주 사용된다.

3D Scaling
uniform scaling vs. non-uniform scaling, simple!

3D Rotation
3차원 회전은 점을 중심으로 하는 2차원 회전과 달리 회전 축(axis of rotation)을 필요로 한다
z축을 중심으로 3차원 공간에 정의된 (x, y, z) 회전 = z좌표는 움직이지 않음 = 2차원 공간에서 (x,y) 회전

z축 기준 3차원 회전 -> x축이 y축 방향으로
x축 기준 3차원 회전 -> y축이 z축 방향으로
3차원 공간에서의 회전을 직관적으로 이해하는 법
= 물체를 바라보는 시점이 회전축과 동일한 방향이다
= 따라서 회전축이 공간에서 사라진다


3차원 회전의 방향: CCW (Counter Clock-wise) vs. CW (Clock-wise)
CCW -> positive angle, \(\theta\)
CW -> negative angle, \(-\theta\)
*note : \(-\theta = 2\pi-\theta\)
3D Translation
simple!
3차원 선형변환에서는 homogeneous coordinates로서 4x4 행렬로 표현하고 연산한다.

Application: World Transform
object space = 하나의 오브젝트를 생성하는데 사용하는 좌표계
어떤 오브젝트를 위한 좌표계(object space)는 또 다른 오브젝트를 위한 좌표계와 상관이 없다.
world space -> 모든 오브젝트 모델들의 위치를 통합하여 표현하는 단일 좌표계
world transform = transform from object space to world space


'3D Computer Graphics > Learnings' 카테고리의 다른 글
| 컴퓨터그래픽스_정점 처리(1) (0) | 2022.04.25 |
|---|---|
| 컴퓨터그래픽스_좌표계와 변환(3) (0) | 2022.04.23 |
| 컴퓨터그래픽스_좌표계와 변환(1) (0) | 2022.04.21 |
| 컴퓨터그래픽스_모델링 (0) | 2022.04.15 |
| 컴퓨터그래픽스_수학 기초 (0) | 2022.04.15 |
- Total
- Today
- Yesterday
- vertex shader
- 컴퓨터그래픽스 좌표계와 변환
- PoseNet
- tensorflow.js
- 원유로필터
- 컴퓨터그래픽스 강의
- 컴퓨터그래픽스
- 3d affine transform
- 고려대학교 한정현
- 메타버스
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
